In Keely's SVP and music: more than one frequency sounded simultaneously. Modern terminology is vibration signature which is a graphical representation of more than one frequency sounded simultaneously or complex waveform.

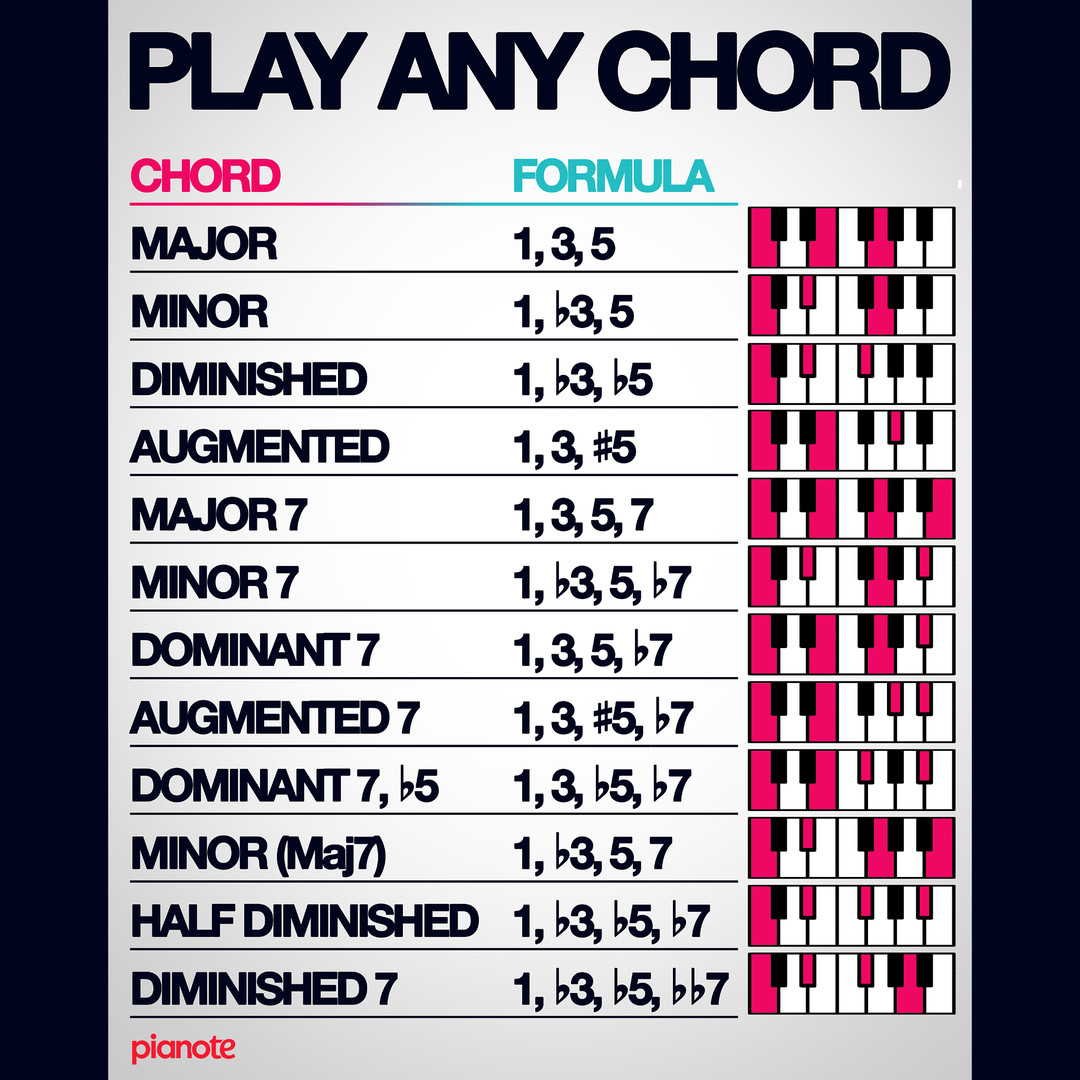
The combination of three or more tones played at once. Diatonic c. uses only notes proper to the key. A triad is a chord of three notes in which the lowest is combined with the third and fifth above it. Common c. is a triad in root position. Dominant c. is founded on the dominant of the key. An inverted c. uses a tone other than the root as its lowest tone. Harmony is the study of chords and their relations.

---

Keely
Chord, Progressive Sympathy "The chords will be set in progressive sympathy from the first octave to the fortieth..." [Keely and His Discoveries]

Chord Center "The difference in the condition of the sympathetic nerve centers, and the variations in the chord aggregation of the masses, as established in the man or woman at birth, constitutes the molecular condition of the individual. The molecular state of animals, vegetables, and minerals depends upon the aggregation of their chord centers." [Keely and His Discoveries, page 222]

Chord of Harmony "The molecular state of animal, vegetable and mineral matter depends upon the aggregation of their respective chord centers. It is impossible to make two coins from the same die the same in their molecular aggregation. To produce vibratory devices will require instruments more perfect than any now in existence. One of my perfected instruments shows to the eye the 'molecular effects' produced by the chord of harmony between two neutral centers. (Lissajous figures?) Another, connected with the 'sympathizer' denotes accurately by the color of the sound (or sound combination) the number of vibrations necessary to induce `certain mechanical combination effects'." The Snell Manuscript

Chord of Mass Sympathy "To illustrate "chord of mass sympathy" Keely filled a glass chamber 40 inches high with water and placed in it three metal spheres each weighing about six ounces, and having the respective mass chords of B flat, first octave E flat, second octave and B flat, third octave, which all rested on the floor of the container.

When B flat, first octave was sounded through the transmitter the positive end of which was attached to the cover, the sphere with the corresponding mass chord rose slowly to the top. Upon changing to the negative it descended as gently as it rose. The other spheres moved likewise on sounding their respective mass chords.

This indicates that the conclusion reached by the Scholastic school is correct, in that: "WHEN ONE BODY ATTRACTS ANOTHER BODY, THE EFFECT IS AGGREGATE, THE RESULT OF ONE WHOLE OPERATING ON ANOTHER WHOLE, AND NOT THE SUM OF THE EFFECTS OF THE PARTS OF ONE ON THE PARTS OF THE OTHER." The Snell Manuscript

"No such thing as discord exists in the molecule. Discordance results from chords producing differentiation and may be equated by the proper chord of harmony. Every gaseous molecule is a resonator to any and all vibrations, whether concordant or discordant. That which we term discord exists in sound itself, not in matter." [Snell Manuscript - the book, DISCORD - Snell]

"Therefore, it is necessary to submit the wire to a system of graduation in order to find what the combined chords of these nodal interferences represent when focalized to one general center. Then the differentiation between these nodal waves and the intermolecular link must be equated, by what I call a process of vibratory induction, so as to induce pure concordance between one and the other. To elaborate on this system of graduation, for effecting conditions necessary to ensure perfect and unadulterated transmission, would make up a book that would take days to read and months to study. [Snell Manuscript - The Book, GRADUATION OF MACHINES, page 5]

"The positive vibrations are the radiating or propulsive, the negative vibrations are the ones that are attracted towards the neutral center. The action of the magnetic flow is dual in its evolutions, both attractive and propulsive. The sound vibrations of themselves have no power whatever to induce dissociation, even in its lowest form. Certain differential, dual, triple and quadruple chords give introductory impulses which excite an action on molecular masses, liquid and gaseous, that increase their range of molecular motion and put them in that receptive state for sympathetic vibratory interchange which favors molecular disintegration, then, as I have shown, the diatonic enharmonic is brought into play, which further increases the molecular range of motion beyond fifty percent of their diameters, when molecular separation takes place, giving the tenuous substance that is necessary to induce progressive subdivision. This molecular gaseous substance, during its evolution, assumes a condition of high rotation in the sphere or tube in which it has been generated, and becomes itself the medium, with the proper exciters, for further progressive dissociation. The exciters include an illuminated revolving prism, condenser, and colored lenses, with a capped glass tube strong enough to carry a pressure of at least one thousand pounds per square inch. To one of these caps a sectional wire of platinum and silver is attached; the other cap is attached to the tube so screwed to the chamber as to allow it to lead to the neutral center of said chamber." [Snell Manuscript - The Book, ANSWERS TO QUESTIONS, page 6]

"In organ pipes, of a certain calibre, very sensitive waves occur at intervals; as according to the character of the sound evolved; but on a combination of resonators composed of brass tubes of more than nine in number, a wave of sound, induced by certain chords passing over them, produces high vortex action of the air enclosed in them. The vibration of tuning forks induces alternate condition of the air that surrounds them, if in open atmosphere; but quite a different action presents itself when the forks are exercised in resonating tubes, set to thirds of the mass chord they represent. Then high vortex action is the instant result. Vibrators cannot be set promiscuously in tubes, and get such results, any more than a musician can render a musical composition on the violin before tuning it." [Appendix I]

With his Generator, which was invented for the purpose of multiplication of vibrations, he secured higher frequencies by disturbance of equilibrium of mediums of different specific gravities, air as one, water as the other.

In the disintegration of water in his "Liberator" he produced the "etheric order of ozone." This he is said to have used in a "carbon register" to produce a high vibratory circuit that proved sufficient to break up cohesion, which he states is simply molecular magnetism. At that time he used, in molecular dissociation, one tuning fork of 620 per second, setting chords on the first octave, in atomic separation, two forks, one of 620 and one of 630, setting chords on the second octave, and in etheric separation used three forks, one of 620, one of 630 and one of 12,000, setting chords on the third octave. [VIBRATORY MULTIPLICATION]

"Electricity is the result of three differentiated sympathetic flows, combining the celestial and terrestrial flows by an order of assimilation negatively attractive in its character. It is one of Nature's efforts to restore attractive differentiation. In analyzing this triple union in its vibratory philosophy, I find the highest order of perfection in this assimilative action of Nature. The whole condition is atomic, and is the introductory one which has an affinity for terrestrial centers, uniting magnetically with the Polar stream, in other words, uniting with the Polar stream by neutral affinity. The magnetic or electric forces of the earth are thus kept in stable equilibrium by this triune force, and the chords of this force may be expressed as:

1st.: The Dominant
2nd.: The Harmonic
3rd.: The Enharmonic. [WHAT IS ELECTRICITY]

"The series of experiments, daily for one week, that I am now preparing to give before an expert committee, for the purpose of enabling this committee to make a public announcement of the scientific and commercial value of my system of sympathetic vibratory physics, comprises:

First. - Operation of the polar circuit, drawing power from space, and showing control of various degrees of velocity.

Second. - Sensitization of a polar disk, after having had its complete neutrality to magnetism tested.

Third. - After associating it with the polar test-medium, heavily weighting it to demonstrate its attractive power; the weight remaining suspended to it by this power.(7)

Fourth. - Transmitter connected to the test-medium, while the disk is carrying the weight. Negative vibration transferred; effecting complete dissociation; the disk and weights dropping to the floor.

Fifth. - Rotation of compass needle, on a set of resonators, subservient to any one of the resonators, in defiance of its attraction to the north. Variations given; changing its subservience to different resonators, as the introductory impulse is changed.(8)

Sixth. - Mediums, representing the chords of different masses of metal, made to float in a tall jar of water, with extraordinary changes of position.

Seventh. - Operations of a sensitized globe, by sound.

Eighth. - Operations of the globe under the influence of the improved polar sympathetic transmitter.

Ninth. - Disintegration of water by triple vibration,(9) showing progressive degrees of energy (from molecular to interatomic, etc., etc.) on different rates of transfer." [The Operation of the Vibratory Circuit]

---

Ramsay
"And as the notes of this family are born of one fundamental note, so the chords into which they are grouped are like so many younger families. The fundamental note is the common root of three chords, each of which is a little family of notes having its own generating root; although the top of the first is the root of the second, and the top of the second, the root of the third. This also is illustrated in the Genesis of the Scale. [Scientific Basis and Build of Music, page 20]

"Of these three chords, which constitute a scale or key, Nature next proceeds to generate, in a similar way, a family of scales or keys, and these in two lines, the Major and the Minor. The twice twelve-fold family of keys is brought forth in much the same way as were the chords which constitute them, and as were the notes which constitute the chords. There is a beautiful growth-like continuity in the production of all." [Scientific Basis and Build of Music, page 20]

"The system of musical sounds is derived from the laws of motion and a particular election of numbers which give the greatest variety of simple ratios.
There are three primary and pregnant ratios which produce the chords and scales. The first is the ratio of 1:2, producing Octaves, and nothing else; the second is the ratio of 2:3, producing Fifths; the third is the ratio of 4:5, producing Thirds." [Scientific Basis and Build of Music, page 26]

this is the middle of our chord, E, G, B; and remember that this also is G as we found it coming upward, C3 multiplied by 3 being G9. This is another note of the minor, the same in its quantity as that of the major. Now for another chord downward we must divide the root of the one we have found, namely E15, by 3, which will give us A5, the root of a center chord for the minor, and the very key-note of the relative minor to C. And remember that this A5 is just as we found it in coming upward, for F multiplied by 5 gave us A5. Now divide E15 by 5 and we have C3, the middle to our minor chord, A, C, E. Still we must remember that this C3 is just as we found it coming upward, for F multiplied by 3 is C3. Behold how thus far major and minor, though inversely developed, are identically the same in their notes, though not in the order in which they stand in the fifths thus generated. [Scientific Basis and Build of Music, page 32]

The life-force of the notes from the law of position gives them a versatility which they could never have had from fixed ratios, however numerous. If the interval of the octave be excepted, there are no two notes together in a chord, nor succeeding each other in the octave scale, having the same amount of specific levity or gravity; consequently each note has an expression and [Scientific Basis and Build of Music, page 35]

When the major scale has been generated, with its three chords, the subdominant, tonic, and dominant, by the primary mathematical ratios, it consists of forms and orders which in themselves are adapted to give outgrowth to other forms and orders by the law of duality and other laws. All the elements, orders, combinations, and progressions in music are the products of natural laws. The law of Ratio gives quantities, form, and organic structure. The law of Duality gives symmetry, producing the minor mode in response to the major in all that belongs to it. The laws of Permutations and Combinations give orders and rhythms to the elements. The law of Affinity gives continuity; continuity gives unity; and unity gives the sweetness of harmony. The law of Position gives the notes and chords their specific levities and gravities; and these two tendencies, the one upward and the other downward, constitute the vital principle of music. This is the spiritual constitution of music which the Peter Bell mathematicians have failed to discern: [Scientific Basis and Build of Music, page 37]

If the effects of notes and chords had depended entirely on their mathematical ratios, then the effect of the subdominant, tonic, and dominant would have been alike; for these three chords have exactly the same ratios. It is the law of position which gives the tonic chord its importance, and not any special ratios embodied in its structure. The ratio of 2 to 1 has a pure, unmixed, invariable character, always realized in the interval of the octave. The notes produced from 1 by the first, second, and third powers of 3 have different degrees of centrifugal force. The character of the notes produced by the first power of 5 depends on the character of the notes from which they are derived, namely, 1, 3, and 9. The final character of the notes and chords derived by the same ratios is determined by the amount of force which they have acquired from the way in which they have been derived, and from their position in the system; and no matter where these notes may afterwards be [Scientific Basis and Build of Music, page 37]

RESOLUTION - The tendency and going of a note of one chord to some note of the next chord. [Scientific Basis and Build of Music, page 40]

It is in their inverse relations that the major and the minor are equal. Every note, chord, and progression in the one has its reciprocal or corresponding note, chord, and progression in the other. This is the Law of Duality. And this general law of Nature is so deeply rooted in music, that is the numbers which represent the vibrations in the major system be made to represent quantities of string, these quantities will produce the minor system (beginning, of course, with the proper notes and numbers); so that when the quantities are minor the tones are major, and when the quantities are major the tones are minor.¹[Scientific Basis and Build of Music, page 44]

in their birthplace - F A C, C E G, G B D. Indeed in their birth not only is it so, but still further, the top note of the first chord is the root and generator of the third. They are linked in generative continuity. [Scientific Basis and Build of Music, page 49]

In the progression - that is, the going on from one to another - of these triplets in harmonizing the octave scale ascending, Nature goes on normally till we come to the passage from the sixth to the seventh note of the scale, whose two chords have no note in common, and a new step has to be taken to link them together. And here the true way is to follow the method of Nature in the birthplace of chords.¹ The root of the subdominant chord, to which the sixth of the octave scale belongs, which then becomes a 4-note chord, and is called the dominant seventh; F, the root of the subdominant F, A, C, is added to G, B, D, the notes of the dominant, which then becomes G, B, D, F; the two chords have now a note in common, and can pass on to the end of the octave scale normally. In going down the octave scale with harmony, the passage from the seventh to the sixth, where this break exists, meets us at the very second step; but following Nature's method again, the top of the dominant goes over to the root of the subdominant, and F, A, C, which has no note in common with G, B, D, becomes D, F, A, C, and is called the subdominant sixth; and continuity being thus established, the harmony then passes on normally to the bottom of the scale, every successive chord being linked to the preceding note by a note in common. [Scientific Basis and Build of Music, page 49]

In the laws of quantities and motions the three primary ratios, 1:2, 1:3, 1:5, with the three different units, F1, C3, and G9, the roots of the chords of the subdominant, tonic, and dominant, produce the three chords of the musical system major, the one not interfering with the other; and by an inverse process are produced, from B720, E240, and A80, its generating notes, the three chords of the musical system minor; the one chord not interfering with the other. In a similar way the chromatic chords can be produced from three different units, without the one interfering with the other; and, like the subdominant, tonic, and dominant chords of the diatonic scale, they are fifths apart. So we may call them the subdominant, tonic, and dominant chromatic chords. Each of the three chromatic chords has also kinship with the major and minor modes, from the way in which the diatonic minor triad is constituted a chromatic chord by its supplement coming in the one side from the minor, and on the other side from the major system. [Scientific Basis and Build of Music, page 53]

[Scientific Basis and Build of Music, page 54]

But, as the subdominant sixth and dominant seventh suggest that the chromatic chord should be a 4-note chord, we must find out how Nature completes this diatonic chromatic triad and makes it a 4-note chord, and that according to its own intrinsic character as of minor thirds. Nature has always a rationale in her operations which it is ever delightful to discover. Wedged in between the minor dominant and the major subdominant, this triad, B D F, has already B, the top of the dominant minor, for its root; and F, the root of the subdominant major, for its top; and its middle is the mysterious D which, in its two positions as root of the minor subdominant and top of the major dominant, stands at the two extremes of the whole twofold diatonic key, bounding and embracing all; and which in its two degrees as D26 2/3 and D27 claims kindred with both minor and major modes of the twofold key system. Surely this Janus-faced D, looking this way toward the minor and that way to the major, seems to say, "the complement of this chord, of which I am the heart, is not far to seek nor hard to find on either side." It has already B in common with the minor dominant; the very next step is to the middle of this chord, G. Roots and tops of chords may not be altered, but middles may with impunity be flattened or sharpened as occasion may require. No two of them in succession in the chord-scale have the same structure; the chromatic triad, in claiming this middle, claims it sharpened, for it must have [Scientific Basis and Build of Music, page 54]

a minor third. So by adding the middle of the minor dominant, G, but made G#, that the third so produced may be a minor third, according to the nature of the chromatic chords, we have on this minor side of the chord G#, B, D, F, which we may call its minor form, inasmuch as the semitone of its second minor third is the one, B-C, which genetically arises in the minor genesis; and inasmuch as it has also received its supplemental G# from the minor dominant. How shall we find its complement on the other side? We have seen that D, the Janus-faced center of this triad, B, D, F, looks, as D27, toward the major also; it has already F in common with the major subdominant. The very next step is to the middle of this chord, A. Middles, we have just seen, are ever ready to accommodate themselves; and this minor third triad claims that A be flattened, for on this side also, though its major side, it must have a minor third; so by adding the middle of the major subdominant, A, but made A?, according to the nature of chromatic intervals, that this F-A? also may be a minor third; and now we have it as B, D, F, A?, which we may call its major form, inasmuch as the semitone of its minor third, E-F, is the one which genetically arises in the major genesis, and inasmuch as it has now received its supplemental A? from the major subdominant. This, then, is the chromatic chord in its native place, and in its native constitution; a 4-note chord, wholly of the minor thirds. It will be observed that it has now, in its two forms, divided the octave into minor thirds - 4 minor thirds, so it is very much at home anywhere in the octave; indeed it is at home everywhere - G#, B, D, F, A?. And as every diatonic common chord in music is constituted of materials found in the octave of notes, it cannot be far from a chromatic chord in some one of its forms. [Scientific Basis and Build of Music, page 55]

being also the center of the diatonic triplet, B, D, F, which is the diatonic germ of the chromatic system. Four minor thirds upward or downward from C# we have a second chromatic chord, its central note being G. The dual¹ of C# is E?; and there is the same order of keys on the keyboard² below C# as there is above E?. Four minor thirds from E? upward or downward forms a third chromatic chord, the central note of which is A. The dual A, the center of the third chromatic, is G, the center of the second; and these two notes, by their duality, and by the duality of the two chords throughout, balance each other exactly on the keyboard on either side of the first chromatic chord, which contains all its own duals, and by this self-duality sits in the center, like the tonic chord among the diatonic three. [Scientific Basis and Build of Music, page 57]

The CHROMATIC SYSTEM of chords is developed from these three primitive chromatic chords, and in the course of its development one or two notes are brought in semitonic progression to the middle, one or two to the root, and one or two to the top of all major and minor tonic chords. Likewise, at one time or another in the course of the system, there is one note in common with the middle, one note in common with the root, and one note in common with the top of all the major and minor tonic chords. [Scientific Basis and Build of Music, page 57]

It is the function of the chromatic chord, in the course of its systematic development, to bring two notes, the one above and the other below, in semitonic progression to each of the three notes of the tonic chord; and likewise, without interfering with the imperial character of the tonic chord, it brings two notes in semitonic progression to each note of the other two chords; so that, although at first the subdominant and dominant chords are only like satellites to the tonic chord, they, with their chromatic chords, are now raised to the dignity of planets as it were, having the chromatic chords as their satellites. [Scientific Basis and Build of Music, page 57]

dividing itself by 2 or 3 or 5, etc., up through the whole geometrical series of numbers, not keeping fixed at one thing; but while the whole length is vibrating the fundamental partial, it keeps shifting the still nodes along its length, and sometimes longer and sometimes shorter segments are sounding the other partials which clothe the chief sound. It has been commonly said that "a musical sound is composed of three sounds," for every ear is capable of hearing these three, and with a little attention a few more than these; but many will be startled when told that there are twenty-five sounds in that sound. Eighteen of them are simply the octaves of the other seven, all of these seven except one having one or more octaves in the sound. Four of the seven also are very feeble, the one which has no octave being the feeblest of all. Two of the other three are so distinctly audible along with the chief partial that they gave rise to the saying we have quoted about a musical sound being composed of three sounds.¹ If the three most pronounced partials were equally developed in one sound, it could not be called one sound - it would decidedly be a chord; and when in the system they do become developed, they form a chord; but in the one sound they, the partials, having fewer and fewer octaves to strengthen them, fade away in the perspective of sound. The sharp seventh, which in the developed system has only one place, not coming into existence until the sixth octave of the genesis, is by far the feeblest of all the partials, and Nature did well to appoint it so. These harmonics are also sometimes called "overtones," because they are higher than the fundamental one, which is the sound among the sounds, as the Bible is the book among books. [Scientific Basis and Build of Music, page 59]

A second cause of difference in degree of contrast between two notes and other two notes in which the ratios are the same lies in this - whether the two notes belong to one chord or to different chords. Two notes in the subdominant chord have a different contrast from two in the dominant chord which have the same ratio. [Scientific Basis and Build of Music, page 61]

Position - The relative place of chords in a key. [Scientific Basis and Build of Music, page 63]

Tetrachord - From tetra, four, and chord. It does not mean a four-note chord, but four notes such as our C, D, E, F. [Scientific Basis and Build of Music, page 63]

We have gone from vibrations to musical notes; from notes to chords; and now we proceed to scales - that is, groups of notes or chords in succession, which are bound and unified in some clear and definite way. [Scientific Basis and Build of Music, page 64]

embedded; and in the minor tonic chord A C E in the same way is embedded its own semitone; and in these chords they appear in their proper places as third and fourth, C, d, E f, G; and second and third, A, b C, d, E. It is these first five notes of the octave scale which in a very distinctive way constitute the natural scale, which can be harmonized consecutively in one manner. The octave is seen in this view to be a compound scale, inasmuch as a compounding method of harmonizing has to be resorted to in passing consecutively from the sixth to the seventh. Similar compounding has to be done in the minor as well.¹ [Scientific Basis and Build of Music, page 65]

Moreover, it is only from one to five, that is from C to G in ascending, which is its proper direction in the genesis, that the major in being harmonized does not admit of minor chords, but if we descend this same natural major scale of the fifth from five to one, that is from G to C, the first chord is C E G; the next chord is F A C; if this is succeeded by the minor chord A C E, there are two notes in common and one semitonic progression, as very facile step in harmony; and the following two notes are most naturally harmonized as minor chords. So modulation into the minor, even in this major scale, is very easy in descending, which is the proper direction of the minor genesis.² In a similar way, it is only from five to one, that is from E to A in descending, which is its proper genetic direction, that the minor in being harmonized does not admit of major chords; but if we ascend this same minor scale of the fifth from one to five, the first chord is A C E, the next is E G B, and if this chord be followed by the major C E G, there are here again two notes in common and one semitonic progression; and the two notes following are then most naturally harmonized as major chords. So modulation into the major, even in this minor scale, is very natural and easy in ascending, which is the proper direction of the major genesis.³ The dominant minor and the tonic major are, like the subdominant major and the tonic minor, very intimately related in having two notes in common and one semitonic progression. [Scientific Basis and Build of Music, page 65]

where there stands an open door between the sixth and the seventh, these two having no note in common, it is easy and natural to slip out of the key into another, either in ascending the major or descending the minor octave; and in order to keep in the key, the two chords of these notes have to reach out to each other a helping hand, and compound in order to affiliate. This, however, by the law of sympathy and assimilation, which reigns in this happy, realm, they are always ready to do.¹ [Scientific Basis and Build of Music, page 66]

This great genetic scale, the all-producer, the all-container, extends over six octaves on each side; for it is not till high in the sixth octave we get B in the major, and it is not till low in the sixth octave that we get F in the minor. It is in the fifth octave, however, that the note which is the distinctive mark of the masculine and feminine modes is generated. D27 in the major, and D26 2/3 in the minor, distinguishes the sex of the modes, and shows which is the head and which the helpmeet in this happy family.² On the major side F, the root of the subdominant chord, that is the chord which is a fifth below the key-note C, is the root of all. This is the beginning of this creation. If we call the vibration-number of F one, for simplicity's sake, then F1 is multiplied by 3 and by 5, which natural process begets its fifth, C, and its third, A; this is the root, top, and middle of the first chord. From this top, C3, grows the next chord by the same natural process, multiplying by 3 and by 5; thus are produced the fifth and third of the second chord, G and E. From the top of this second chord grows the third and last chord, by the repetition of the same natural process; multiplying G9 by 3 and by 5 we [Scientific Basis and Build of Music, page 66]

Now we come to a remarkable arrangement of Nature. The minor does not grow in the same way out of this third chord's top. Two features come before us: first the minor chord grows out of the major, but it is taken not from the top but from the middle, from a rib out of his side. B, the middle of the major dominant chord; B, the last-born of the major genesis; B is the point of departure in the outgrowth of the minor mode. The feminine is a lateral growth from the masculine. Another feature: it grows downward, like a drooping ash or willow. Its first generated chord is its dominant, and its last is its subdominant. Its middle chord, like the middle one of the major, is its tonic. Still further, it is generated by division, not multiplication; B45 is divided by 3 and by 5 for the root and middle of this highest chord, E and G. E15 is divided by 3 and 5 for the root and middle of the tonic chord, A and C. A5 is divided by 3 and 5 for the root and middle of the lowest chord, D and F. Thus we have the whole generation of the elements of music, six generations of harmony, like the six days of creation. Up to this point the whole process and aspect is inverse; growing from a middle; growing downward; growing by division;- while the major is growing from the top; growing upward; growing by multiplication. But here the inverse aspect ends. The generating primes of the major are 3 and 5; 3 and 5 are also the generating primes of the minor. In this essential phase of their creation their comparison is direct, not inverse. [Scientific Basis and Build of Music, page 67]

Music, and mathematics have nothing more to do with it. Already the Law of Position has guided the genesis upward in the major; and while mathematical primes were generating the chords one after another in precisely the same way and form, like peas in a pod, the Law of Position was arranging them one over the other, and so appointing them in their relative position each its own peculiar musical effect bright and brighter. And when the major had been thus evolved and arranged by ratios and position, another law, the Law of Duality, gave the mathematical operation its downward direction in the minor; and while the primes which measured the upward fifths of the major also measure the downward fifths of the minor, the Law of Position is placing them in their relative position, and appointing each its own peculiar effect grave and graver. [Scientific Basis and Build of Music, page 68]

Chords in a harmony are not at liberty to succeed each other in the way that single notes in a melody may. The notes in a melody may succeed in seconds, or they may succeed in larger intervals, any interval in the octave, even sometimes very effectively there may be a leap or fall of a whole octave. Chords cannot follow each other in this free way; they are under law, and must succeed accordingly. Their law is that they must be linked together either by having something in common in their elements, or have small intervals, semitonic progressions, between them. The former way, by notes in common, is the most usual way in diatonic succession of chords, the latter way, by semitonic progression, is a chief feature and charm in chromatic succession; but both in diatonic and chromatic progression of chords in harmony, notes in common and semitonic progression are usually found together. [Scientific Basis and Build of Music, page 68]

The Chromatic Scale is naturally the last to come into view, for it is not generated by a mathematical process at all. Chromatic intervals are indeed found in the scale as mathematically generated. The semitones between B-C and E-F are two chromatic intervals, and the chord which occurs between the major and the minor in the chord-scale when it begins with the minor mode is a chromatic chord, though in an uncompleted condition. But the making of the octave into a chromatic scale of twelve small or semi-tones, is the work of modulation from one key to another through the whole twelve keys in either the major or minor sphere; and this process is fully set forth in the pre-note to the chromatic treatise. [Scientific Basis and Build of Music, page 69]

The number of Diatonic Chords. In the major there are three simple chords, two compound chords, and two double compound, seven in all - subdominant, tonic, dominant, subdominant sixth, subdominant fourth, dominant seventh, and dominant ninth. In the minor there are the same number and order, making fourteen. It is not normal to the tonic chord to compound, but it may, in exceptional instances; the major tonic may, in a certain cadence, assume the top of the minor subdominant; and the minor tonic may assume, in a cognate case, the root of the major dominant.¹ [Scientific Basis and Build of Music, page 70]

All compound and double compound chords are made up of notes already developed for the simple chords; there is no genetic developing of compound chords. Simple chords are all begotten in the genesis; they are true species; compound chords are only varieties of them. [Scientific Basis and Build of Music, page 70]

Why do we compound? Because it produces variety, and variety is one of the aspects of the beautiful; Nature loves and abounds in variety, without violation of her unity. And further, all creation throbs with sympathy, one thing feeling and tending toward another, nothing content in isolation; and compound chords are chords reaching out after assimilation to an affiliation with other adjacent chords, that they may be able, through something in [Scientific Basis and Build of Music, page 70]

common, to mingle with more chord-society. So those added thirds which constitute compound chords are like accomplishments acquired for this end, and they make such chords exceedingly interesting. The dominant assumes the root of the subdominant, and so becomes the dominant seventh that it may be affiliated with the subdominant chords. Inversely, the subdominant assumes the top of the dominant chord that it may be affiliated with the dominant. The major tonic may exceptionally be compounded with the top of the minor subdominant when it comes between that chord and its own dominant; and the minor tonic may in the same way assume the root of the major dominant when it comes between that chord and its subdominant. The minor subdominant D F A, and the major dominant G B D, are too great strangers to affiliate without some chord to introduce them; they seem to have one note in common, indeed, but we know that even these two D's are a comma apart, although one piano-key plays them both, and the F G and the A B are as foreign to each other as two seconds can be, each pair being 9 commas apart, and G A are 8 commas apart. In this case, as a matter of musical courtesy, the tonic chord comes in between; and when it is the minor subdominant that is to be introduced, the major tonic assumes the top of that chord, and then turns to its own major dominant and suavely gives the two to enter into fellowship; for the tonic received the minor subdominant through its semitonic E F, and carries it to the major dominant through its semitonic B C, along with C in common on the one side and G in common on the other. When it is the major dominant that is to be introduced to the minor subdominant the minor tonic fulfills the function, only the details are all reversed; it assumes the root of dominant, and by this note in common, and its A in common with its own subdominant, along with the semitonic second B C on the one hand and the semitonic E F on the other, all is made smooth and continuous. The whole of this mediatorial intervention on the part of the tonic is under the wondrous law of assimilation, which is the law of laws all through creation; but when the tonic chord has fulfilled this graceful action, it immediately drops the assumed note, and closes the cadence in its own simple form.¹ [Scientific Basis and Build of Music, page 71]

How far does this compounding process go? The dominant seventh has the first note of the subdominant; the dominant ninth has the second; if we should add a third note, where are we? G B D F A C; here would be the dominant with the whole of the subdominant welded to it; it would have to be called the dominant eleventh, and it has brought us right through to the root of the tonic C. What would be the use of such a chord? We might, in a similar way, add the dominant to the subdominant till we should be through to the tonic on the other side; it would be G B D F A C, and so we should have reached the top of the tonic G. This process shows us, however, that there is just a certain length that we can go, and there is satisfaction in seeing exhaustively that so it is. When the beautiful becomes the useless, it ceases to be the beautiful. [Scientific Basis and Build of Music, page 72]

The varied effect of position in chords. When a chord stands as C E G C, having its root also at the top, it has its softest, dullest, most united effect; it is undramatic, with little contrast. When it stands as E G C E, having its third at the top and bottom, it has a more ticklish, interesting, far-away effect. In reveries composers often finish thus, as if it had vanished - an unsettled effect. When it stands as G C E G, with its top at top and bottom, it has its most dominant character - loud, swelling. In the position C E G C it stands mixingly with the subdominant C E f G a C, and in this its first position its unseen filling in is chiefly from the region of gravity; hence its soft, grave, dull, heavy effect; and it passes very easily to the subdominant chord. When it stands as G C E G it stands mixingly with the dominant G b C d E G, and has its third position and most brilliant effect and uprising, for its unseen filling in is then chiefly from the region of levity; and it passes easily to the dominant chord. When in its second position, its middle position E G C E, its unseen filling in is mixingly both subdominant and dominant, E f G a b C d E; it has then its most interesting and puzzling effect; on the one hand its softest, dullest, and one-est, on the other hand its most brilliant effect, as if it would at once both sink and soar. [Scientific Basis and Build of Music, page 72]

less variety of effect than we find in the diatonic chords; for although these chords may appear with their notes diversely named, there are still only the three. On account of their cosmopolitan character they need, and they have, no compounding with anything else. They are themselves at home everywhere; like a universal joint, they can turn any way, and affiliate in all directions. Being 4-note chords, and all of minor thirds, their effect is always minor, and they fall with loving softness to the diatonic chords to which they resolve. How this chord in its germ is found in the diatonic chord-scale; how it becomes a 4-note chord of minor thirds; how it variously resolves, each one of the three, in three manners with 24 tonic chords - all this is so fully set forth in the pre-note and treatise on the chromatic chord that it need not be more discussed in this place. See also Plates XVI., XVII., XVIII., XIX., and XX. [Scientific Basis and Build of Music, page 73]

There is nothing extraordinary in this. It is another fact which gives this one its importance, and that is that the musical system is composed of three fifths rising one out of another; so this note by 3/4 becomes the root not only of a chord, but the root of all the three chords, of which the middle one is the tonic; the chord of the balance of the system, the chord of the key; the one out of which it grows, and the one which grows out of it, being like the scales which sway on this central balance-beam. Thus F takes its place, C in the center, and G above. These are the 3 fifths of the system on its masculine or major side. The fractions for A, E, and B, the middle notes of the three chords, are 4/5, 3/5, and 8/15; this too tells a tale; 5 is a new ingredient; and as 3 gives fifths, 5 gives thirds. From these two primes, 3 and 5, along with the integer or unit, all the notes of the system are evolved, the octaves of all being always found by 2. When the whole system has been evolved, the numbers which are the lengths of the strings in the masculine or major mode are the numbers of the vibrations of the notes of the feminine or minor mode; and the string-length-numbers of the minor or feminine are the vibration-numbers of the notes of the major or masculine mode. These two numbers, the one for lengths and one for vibrations, when multiplied into each other, make in every case 720; the octave of 360, the number of the degrees of the circle. [Scientific Basis and Build of Music, page 76]

At the first, in the laws of quantities and motions adjusting musical vibrations, there is one chord of the three notes, F, A, C, the root, middle, and top of the five notes which compose the true natural scale; this one chord can be reproduced a fifth higher, C, E, G, in the same mathematical form, taking the top of the first for the root of the second chord. In like manner this second can be reproduced another fifth higher, G, B, D, still in the same mathematical form, and so fit to be a member of the chord-scale of a key. But the law does not admit of another reproduction without interfering with the first chord, so that a fourth fifth produces no new effect; but the whole key is simply a fifth higher, i.e., if the fourth fifth has been properly produced by multiplying the top of the third fifth by 3 and by 5, the generating primes in music. That this carries us into a new scale is seen in that the F is no longer the F? but F#, and the A is no longer A? but A,. But if we suppose the fourth fifth to be simply the old notes with their own vibration numbers, then D, F, A would not be a fifth belonging either to the major or the minor mode, but a fifth a comma less. The letters of it would read like the minor subdominant, D, F, A; but the intervals, as found in the upward development of the major genesis, instead of being, when expressed in commas, 9, 5, 8, 9, which is the minor subdominant, would be 8, 5, 9, 8, which is not a fifth of the musical system; these having always, whether major or minor, two 9's, one [Scientific Basis and Build of Music, page 77]

In compound chords there are no new notes created; they are found by combining the notes of the simple chords. The dominant sevenths, major and minor, are compounded by adding one from the subdominant. [Scientific Basis and Build of Music, page 79]

All the inverse and reciprocal orders in music, whether of notes or chords, are produced by the law of Duality, and this gives them inevitably their symmetrical form. [Scientific Basis and Build of Music, page 79]

If we may add a note to a chord, we may also vice versa add that chord to that note. If we may add F to the dominant chord G B D f, we may add the dominant chord to F, thus, g b d F, in some other [Scientific Basis and Build of Music, page 80]

Having found the framework of the major scale by multiplying F1 three times by 3, find the framework of the minor by dividing three times by 3. But what shall we divide? Well, F1 is the unbegotten of the 25 notes of the great genetic scale; B45 is the last-born of the same scale. We multiply upward from F1 for the major; divide downward from B45 for the minor. Again, B45 is the middle of the top chord of the major system, a minor third below D, the top of that chord, and the top of the whole major chord-scale, so B is the relative minor to it. Now since the minor is to be seen as the INVERSE of the major, the whole process must be inverse. Divide instead of multiply! Divide from the top chord instead of multiply from the bottom chord. Divide from the top of the minor dominant instead of multiply from the root of the major subdominant. This will give the framework of the minor system, B45/3 = E15/3 = A5/3 = D1 2/3. But as 1 2/3 is not easily compared with D27 of the major, take a higher octave of B and divide from it. Two times B45 is B90, and two times B90 is B180, and two times B180 is B360, the number of the degrees of a circle, and two times B360 is B720; all these are simply octaves of B, and do not in the least alter the character of that note; now B720/3 is = E240/3 = A80/3 = D26 2/3. And now comparing D27 found from F1, and D26 2/3 found from B720, we see that while E240 is the same both ways, and also A80, yet D26 2/3 is a comma lower than D27. This is the note which is the center of the dual system, and it is itself a dual note befittingly. [Scientific Basis and Build of Music, page 81]

The chords of the scale are S F A C, T C E G, D G B D. Now D is the top of the dominant. Well, take it as D27 or D54 it is all the same, higher or lower octave.
                         D27                                           D27
                           3                                               5
                     2) 81         A,                             2)185       F#
                     2) 40 1/2   A,                             2) 67 1/2  F#
                         20 1/4   A,                                  33 3/4 F# [Scientific Basis and Build of Music, page 82]

The effects of different positions of chords. The first position is clear and solid; the second is light and pretty. The notes which have the most varied effect in a stream of harmony are the upper and under notes, the edges of the stream; the two outlines determine the effect:-

[Scientific Basis and Build of Music, page 84]

When the chords follow each other placed in such a way as to bring the upper note of the one as near the upper note of the next as it can be, the upper surface of this stream of harmony is the melodic scale and the harmony is the bottom and the body of the stream.

[Scientific Basis and Build of Music, page 88]

In a musical air or harmony, i.e., when once a key has been instituted in the ear, all the various notes and chords seem animated and imbued with tendency and motion; and the center of attraction and repose is the tonic, i.e., the key-note or key-chord. The moving notes have certain leanings or attractions to other notes. These leanings are from two causes, local proximity and native affinity. The attraction of native affinity arises from the birth and kindred of the notes as seen in the six-octave genesis, and pertains to their harmonic combinations. The attraction of local proximity arises from the way the notes are marshalled compactly in the octave scale which appears at the head of the genesis, and pertains to their melodic succession. In this last scale the proximites are diverse; the 53 commas of the octave being so divided as to give larger and lesser distances between the notes; and of course the attraction of proximity is strongest between the nearest; a note will prefer to move 5 commas rather than 8 or 9 commas to find rest. Thus far PROXIMITY. [Scientific Basis and Build of Music, page 91]

By affinity the notes group in chords. The tonic is the center chord, the key of the harmony; the dominant is the fifth above it and the subdominant the fifth below it, and these two are balanced on the center chord as the scales on a balance beam. The dominant chord is vigorous and active, tending to soar; the subdominant is solemn, soft, and grave, tending to sink; the tonic is melodious and restful, and in it the harmony finds equilibrium. This far AFFINITY. [Scientific Basis and Build of Music, page 91]

Thus chord tends toward chord, and note leans toward note, and it has to be considered whether the attraction of affinity or proximity be strongest while working out the charming effects of a composition. [Scientific Basis and Build of Music, page 92]

In passing from one key to another in the fellowship of keys in a composition, the new key grows out of the top of the dominant and converts the old dominant into a tonic. The dominant and subdominant being at the opposite extremes of the key, with the tonic between them, are not related by affinity. This want of affinity makes an opening in the system for the new chord to come in by, and it, being related by affinity to the chord of the old dominant, which is now the new Tonic, comes in and establishes itself and the new key for the time. It is this gap between subdominant and dominant, along with the affinity existing between the new key and the old dominant, which makes this musical event to be so gracefully accomplished. This is what is called natural modulation, the passing for a time into another key in the course of a composition; and its abundant and habitual use in music, even in the simplest chorales, shows how natural and acceptable it is. The young student will find illustrations in the second lines of the Psalm tunes - Watchman, Sicily, Tranquility, Eaton, Birmingham, Jackson, Bethel, Bedford, and Sheffield. Take Watchman, for example, and let the young student follow carefully, noting each chord of the little passage, which we shall analyse for his help. It is by such practice that he will become by-and-by familiar with the kinship of keys and the legitimate resources of harmony. [Scientific Basis and Build of Music, page 93]

This tune is in the key of E? Major, and the key into which it moves for a passage is the next above it, B? Major. The first chord, E? G B?, is the tonic; the second and third are the tonic and dominant; the fourth, C E? G, whose full form would be C E? G B?, is the compound subdominant of the new key, which suggests the approaching modulation. The next two chords, in which the measure closes, may either be viewed as the tonic and dominant of the key, or the subdominant and tonic of the new key. The second measure opens with the same chord which closes the first measure, and is best defined as the tonic of the new key; the second chord is clearly the dominant of the new key, and the whole of the second measure is in the new key, and reads, T. D. S. T. compound D. T. Some of these chords might be read as chords of the old key, so near to each other and so kindred are the contiguous keys. All contiguous keys to a certain extent overlap each other, so that some of the chords may be variously read as belonging to the one or to the other. [Scientific Basis and Build of Music, page 94]

In the opening of the third measure the tune returns to its own key by striking the tonic. This case is a very simple illustration of how a composition will move with perfect naturalness in more keys than one, the keys so grow out of each other, and may either merely snatch a passing chord from a new key, or pass quite into it for a phrase or two, or for a whole measure, then return as naturally, either by a smooth and quiet or by a strongly contrasted turn, according to the chords between which the turn takes place. In such modulation there may or there may not be marked a sharp, ?, or ?, in the air itself; the note which Nature raises in the new key may occur in one of the other parts of the harmony. In Watchman it is A, the fourth, which is altered; from being ? it is made ?. The change which takes place in the sixth of the scale, which is C in Watchman, is only one comma, the ratio of 80 to 81, and it slips into the new key as if nothing had happened. No mark is placed to it, as the comma difference is never taken notice of, although it is really and regularly taking place, with all the precision of Nature, in every new key. It is, however, only the note which is altered four commas, which is marked by a sharp, ?, or ?, as the case may be. [Scientific Basis and Build of Music, page 94]

"The organic structure of music is formed by the three ratios of 1:2, 1:3, and 1:5, from the laws of quantities and motions; but as it is only the ratio of 1:2 that has a pure, unmixed, invariable character, and as the notes produced by the first, second, and third powers of THREE have different degrees of centrifugal force, and the character of the notes produced by the first power of FIVE depends on the character of the notes from which they are derived, so the final character of the notes and chords is determined by the amount of force which they have acquired from the way in which they have been derived, and from their position in the system; and no matter how these notes may be afterwards placed, like chemical elements, they never lose their original force. [Scientific Basis and Build of Music, page 95]

- and it is balanced between the two forces. If the effects of notes or chords depended solely on their ratios, then the effect of the subdominant, tonic, and dominant would have been alike, for these chords have exactly the same ratios. The centrifugal force of the notes of the dominant chord would take if away from the tonic chord; but Nature, in her skill to build and mix, has in the octave scale placed the middle of the dominant B under the root of the tonic C, and the top of the dominant D under the middle of the tonic E; so that these two rising notes are inevitably resolved into the tonic chord. The gravitating tendencies of the notes of the subdominant would take it also away from the tonic; but in the octave scale Nature has placed the middle of the subdominant A above the top of the tonic G, and the root of the subdominant F above the middle of the tonic E; so that these two falling notes also are inevitably resolved into the tonic chord. In this way two notes resolve to the center of the tonic, D upwards and F downwards; one to the top, A to G, and one to the root, B to C. Nature has thus placed the notes which have upward tendencies under the notes having downward tendencies; she has also related them by proximity, the distance from the one to the other being always either a semitone or the small tone of the ratio 9:10. [Scientific Basis and Build of Music, page 95]

The System of Musical Sounds might be sketched as follows:- Three different notes having the simplest relations to each other, when combined, form a chord; and three of these chords, the one built up above the other, form a system. [Scientific Basis and Build of Music, page 96]

The middle one of these three chords is called the tonic; the chord above is called the dominant; and the chord below is called the subdominant. The order in which these three chords contribute to form the octave scale is as follows:- The first note of the scale is the root of the tonic; the second is the [Scientific Basis and Build of Music, page 96]

In the first six chords of the scale the tonic is the first of each two. The tonic chord alternating with the other two produces an order of twos, as - tonic dominant, tonic subdominant, tonic subdominant. The first three notes of the octave scale are derived from the root, the top, and the middle of the tonic dominant and tonic; the second three are derived from the root, top, and middle of the subdominant, tonic, and subdominant. The roots, tops, and middles of the chords occurring as they do produce an order of threes, as - root, top, middle; root, top, middle. The first, third, fifth, and eighth of the scale are from the tonic chord; the second and seventh from the dominant; and the fourth and sixth from the subdominant. In the first two chords of the scale the tonic precedes the dominant; in the second two, the subdominant; and in the third two the tonic again precedes the subdominant; and as the top of the subdominant chord is the root of the tonic, and the top of the tonic the root of the dominant, this links these chords together by their roots and tops. The second chord has the top of the first, the third has the root of the second, the fourth has the root of the third, the fifth has the top of the fourth, and the sixth has the root of the fifth; and in this way these successive chords are woven together. The only place of the octave scale where there are two middles of chords beside each other is at the sixth and seventh. The seventh note of the octave scale is the middle of the dominant, and the sixth is the middle of the subdominant. These two chords, though both united to the tonic, which stands between them, are not united to each other by having a note in common, inasmuch as they stand at the extremities of the system; and since they must be enabled to succeed each other in musical progression, Nature has a beautiful way of giving them a note in common by which to do so - adding the root of the subdominant to the top of the dominant, or the top of the dominant to the root of the subdominant, and this gives natural origin to compound chords. The tonic chord, being the center one of the three chords, is connected with the other two, and may follow the dominant and sub- [Scientific Basis and Build of Music, page 97]

dominant; and either of these chords may also follow the tonic; but when the dominant follows the subdominant, as they have no note in common, the root of the subdominant is added to the dominant chord, and this forms the dominant seventh; and when the subdominant follows the dominant, the top of the dominant is added to the subdominant, and this forms the subdominant sixth. The sixth and seventh of the octave scale is the only place these two compound chords are positively required; but from their modifying and resolvable character they are very generally used. When the dominant is compounded by having the root of the subdominant, its specific effect is considerably lower; and when the subdominant is compounded by having the top of the dominant, its specific effect is considerably higher. In the octave scale the notes of the subdominant and dominant chords are placed round the notes of the tonic chord in such a way was to give the greatest amount of contrast between their notes and the tonic notes. In the tonic chord the note which has the greatest amount of specific gravity is its root; and in the octave scale it has below it the middle and above it the top of the dominant, the two notes which have the greatest amount of specific levity; and in the octave scale it has above it the middle and below it the root of the subdominant - the two notes which the greatest amount of specific gravity. The third note of the scale, the middle of the tonic chord, is the center of the system, and is the note which has the least tendency either upwards or downwards, and it has above it the root of the subdominant, the note which has the greatest amount of specific gravity, and it has below it the top of the dominant, the note which has the greatest amount of specific levity. Thus the root of the subdominant is placed above, and the top of the dominant below, the center of the system; the specific gravity of the one above and the specific levity of the one below cause them to move in the direction of the center. [Scientific Basis and Build of Music, page 98]

notes attracted by proximity are attracted in the direction of the center of the tonic chord, major or minor. But if D in the major is attracted by C, the root of the tonic, then it would be moving away from the center. Two notes which have the ratio of 8:9, as C and D, or two notes which are produced by the same ratio as C and D, or two notes where each of them is either a root or a top, as C and D, never resolve to each other by proximity. It is an invariable order that one of the notes should be the middle of a chord. [Scientific Basis and Build of Music, page 99]

Whenever a sharp comes in in making a new key - that is, the last sharp necessary to make the new key - the middle of the chord in major keys with sharps is raised by the sharp, and the top of the same chord by a comma. Thus when pausing from the key of C to the key of G, when F is made sharp A is raised a comma. When C is made sharp in the key of D, then E is raised a comma, and you can use the first open string. When G is made sharp for the key of A, then B is raised a comma. When D is made sharp for the key of E, then F# is raised a comma; so that in the key of G you can use all the open strings except the first - that is, E. In the key of D you can use all the open strings. In the key of A you can use the first, second, and third strings open, but not the fourth, as G is sharp. In the key of E you can use the first and second open. [Scientific Basis and Build of Music, page 100]

The intervening chord between the Diatonic and Chromatic systems, B, D, F. - This chord, which has suffered expatriation from the society of perfect chords, is nevertheless as perfect in its own place and way as any. From its peculiar relation to both major and minor, and to both diatonic and chromatic things, it is a specially interesting triad. F, which is the genetic root of all, and distinctively the root of major subdominant, has here come to the top by the prime 2. D, here in the middle, is diatonically the top of the major dominant, and the root of the minor subdominant; and on account of its self-duality, the most interesting note of all; begotten in the great genesis by the prime 3. B, the last-begotten in the diatonic genesis, top of the diatonic minor, middle of the dominant major, and begotten by the prime 5, is here the quasi root of this triad, which in view of all this is a remarkable summation of things. This B, D, F is the mors janua vitae in music, for it is in a manner the death of diatonic chords, being neither a perfect major nor a perfect minor chord; yet it is the birth and life of the chromatic phase of music. In attracting and assimilating to itself the elements by which it becomes a full chromatic chord, it gives the minor dominant the G# which we so often see in use, and never see explained; and it gives the major subdominant a corresponding A?, less frequently used. It is quite clear that this chromatic chord in either its major phase as B, D, F, A?, or its minor phase as G#, B, D, F, is as natural and legitimate in music as anything else; and like the diatonic chords, major and minor, it is one of three, exactly like itself, into which the octave of semitones is perfectly divided. [Scientific Basis and Build of Music, page 101]

together on radial lines from the center they appear grouped in various chords and combinations, dropping out and coming in in such succession as to constitute what Ramsay, whose genius was given to set this thus before us, calls "Nature's Grand Fugue." Beginning at F in the center at the top, and moving either to the right or to the left, after a run of 7 notes we have 4 consecutive Octaves, and then comes the Minor fifth, A-E, followed by the Major fifth, G-D; and this by another Major fifth, F-C; the combinations keep changing till at the quarter of the circle we come to F, A, C, E, G, a combination of the subdominant and tonic Major; and after another varied series of combinations we have at the half of the circle the elements of 2 minor chords, D, F, A and A, C, E, and one Major chord, C, E, G; at the third quarter we have a repetition of the first quarter group; and the various chords and combinations dropping out and coming in, fugue-like; finally we return to where we began, and end with the three-times-three chord, in which the whole 25 notes are struck together, and make that wondrous and restful close of this strange Fugue. No one can hear the thrice-threefold chord of this close and ever forget it; it is "the lost chord" found; and leads the saintly heart away to the Three in One who is the Lord of Hosts; Maker of Heaven and Earth, and all the host of them. [Scientific Basis and Build of Music, page 103]

In Fig. 1, the mathematical framework of the scales major and minor, is shown the genesis of the scale. F1, in the top figure, is multiplied by 3, and that by 3, and that by 3, which brings us to D27, top of the major dominant. F1 is the root of the whole system. C3 is the top of the first chord, and from that grows the next, and from that the next; and so we have F, C, G, and D, the tops and roots of the major system of chords. When these 3 roots are each multiplied once by 5, the middles of the chords are found, as shown - A, E, and B; so B is the last-born of the major family. When B is taken 4 octaves higher at the number 720 and divided by 3, and that by 3, and that by 3, we get the notes E, A, and D, which are the roots and tops of the minor system of chords. Dividing B, E, and A each by 5 once, we get the middles of the 3 minor chords, as shown. [Scientific Basis and Build of Music, page 103]

Here on the keyboard we see, nearest to the front, the great 3-times-3 chord of the full genesis of the scale from F1 to F64. When this chord is struck by the notched lath represented in front of the keyboard, the whole harmony of the key is heard at once. Behind this great chord are placed, to the left the subdominant, tonic, and dominant chords of the minor. D F A, A E C, E G B; and to the right the subdominant, tonic, and dominant chords of the major, F A C, C E G, G B D. When the notched lath is shifted from F to D, the minor third below F, and the 3-times-3 minor is struck down in the same way as the major, the whole harmony is heard; and the complete contrast of effect between major and minor harmony can be fully pronounced to the ear by this means. Behind these six diatonic chords, major and minor, on the part of the keyboard nearest to the black keys, are the three chromatic chords in their four-foldness, in both major and minor form. The center one shows the diatonic germ of the chromatic chord, with its supplement of G# on the one hand completing its minor form, and its supplement of A? on the other hand completing its major form. A great deal of teaching may be illustrated by this plate.

[Scientific Basis and Build of Music, page 104]

Fig. 1 - The pendulums in this illustration are suspended from points determined by the division of the Octave into Commas; the comma-measured chords of the Major key being S, 9, 8, 9, 5; T, 9, 8, 5, 9; D, 8, 9, 5, 9. The pendulums suspended from these points are tuned, as to length, to swing the mathematical ratios of the Diatonic scale. The longest pendulum is F, the chords being properly arranged with the subdominant, tonic, and dominant, the lowest, center, and upper chords respectively. Although in "Nature's Grand Fugue" there are 25 pendulums engaged, as will be seen by reference to it, yet for the area of a single key 13 pendulums, as here set forth, are all that are required. It will not fail to be observed that thus arranged, according to the law of the genesis of the scale, they form a beautiful curve, probably the curve of a falling projectile. It is an exceedingly interesting sight to watch the unfailing coincidences of the pendulums perfectly tuned, when started in pairs such as F4, A5, and C6; or started all together and seen in their manifold manner of working. The eye is then treated to a sight, in this solemn silent harp, of the order in which the vibrations of sounding instruments play their sweet coincidences on the drum of the delighted ear; and these two "art senses," the eye and the ear, keep good company. Fig. 2 is an illustration of the correct definition of a Pendulum Oscillation, as defined in this work. In watching the swinging pendulums, it will be observed that the coincidences [Scientific Basis and Build of Music, page 104]

The Plate shows the Twelve Major and Minor Scales, with the three chords of their harmony - subdominant, tonic, and dominant; the tonic chord being always the center one. The straight lines of the three squares inside the stave embrace the chords of the major scales, which are read toward the right; e.g., F, C, G - these are the roots of the three chords F A C, C E G, G B D. The tonic chord of the scale of C becomes the subdominant chord of the scale of G, etc., all round. The curved lines of the ellipse embrace the three chords of the successive scales; e.g., D, A, E - these are the roots of the three chords D F A, A C E, E G B. The tonic chord of the scale of A becomes the subdominant of the scale of E, etc., all round. The sixth scale of the Majors may be written B with 5 sharps, and then is followed by F with 6 sharps, and this by C with 7 sharps, and so on all in sharps; and in this case the twelfth key would be E with 11 sharps; but, to simplify the signature, at B we can change the writing into C, this would be followed by G with 6 flats, and then the signature dropping one flat at every new key becomes a simpler expression; and at the twelfth key, instead of E with 11 sharps we have F with only one flat. Similarly, the Minors make a change from sharps to flats; and at the twelfth key, instead of C with 11 sharps we have D with one flat. The young student, for whose help these pictorial illustrations are chiefly prepared, must observe, however, that this is only a matter of musical orthography, and does not practically affect the music itself. When he comes to the study of the mathematical scales, he will be brought in sight of the exact very small difference between this B and C?, or this F# and G?; but meanwhile there is no difference for him. [Scientific Basis and Build of Music, page 108]

Under the symbol of a music plant this plate gives us to realize the growth-like continuity of chords and scales. The roots of the three chords of a key are represented in F, C, and G of the key of C. The plant might be represented as a creeping stem, like the creepers of the strawberry, with its progressive roots struck into the earth; but it is better to show an upward stem with aerial roots, for such are the roots of the musical plant. The main stem of the plant has the three chords, F a C e G b D; that is, F a c, C e g, G b d, the subdominant, tonic, and dominant. The terminal chord, D f# a, is to show that the keys as well as the chords GROW out of each other. Include the side branches which terminate with the octave notes of the chords, read thus - F a c f, G e g e, G b d g, because a chord is felt to be most complete in its unity when thus shut in by the octave note of its root. This is the reason why the great three-times-three chord does not stop at D, the top of the dominant chord, but goes on to the sixth octave of the fundamental root, shutting all in by the great peacemaker, F, in order to preserve the unity of the effect which this chord of chords produces. Before D. C. Ramsay showed that the scale of Harmonics extended to six octaves, it was by teachers of the science of music only extended to four. [Scientific Basis and Build of Music, page 110]

In the major system, when the tonic chord follows the subdominant one, there is one semitonic progression to the middle of the tonic, and one note in common with the root, so these two chords are linked together in different ways. When the tonic chord follows the dominant one, there is one semitonic progression to the root of the tonic, and one note in common with its top, so these two chords also are linked together in two different ways. When the tonic chord follows the compound dominant, i.e., the dominant seventh, there are two semitonic progressions, one to the middle and one to the root, and one note in common with its top, so these two are linked together in the same two ways; but the semitonic progression being double gives this resolution great urgency. And now we come to the two chords, the subdominant and dominant, which have no note in common, and must, when they succeed each other, be helped to come together. Nature teaches us how this is to be done by a process of borrowing and lending which will establish between them a similar relationship to that which keeps the continuity of the other chords in succession. We have seen that the top of the subdominant and the root of the tonic are a note in common to these chords, and so the top of the tonic and the root of the dominant also are a note possessed in common by these two chords. In like manner in this disjunct part, when the dominant follows the subdominant, the root of the subdominant is lent to the top of the dominant, and thus they come to have a note in common. The top of the [Scientific Basis and Build of Music, page 111]

With perfect duality of response does resolution of chords go on in the minors. When the tonic chord follows the subdominant one, they have for their note in common A, i.e., in the key of A; and the middle of the subdominant moves by semitonic progression to the top of the tonic. When the tonic chord follows the dominant one, the top of the tonic and the root of dominant E is a note in common, and the top of the dominant goes by semitonic progression to the middle of the tonic. These simple chords are thus linked together exactly with the same degree of continuity as the simple chords of the major. When the tonic chord follows the compound subdominant, this compound chord, like the compound dominant in the major, has two semitonic progressions - one to the top and one to the middle of the tonic - and they have one note in common. When the compound dominant follows the subdominant, the root of the subdominant is lent to the top of the dominant, and thus a note in common is created, and the middle of the subdominant moves by semitonic progression to the root of the dominant. When the compound subdominant follows the dominant, the top is lent to the root of the subdominant, creating a note in common between them, and the root of the dominant goes to the middle of the subdominant in semitonic progression. This is the way of Nature. The unbroken continuity of her ways is perfectly illustrated in the linked sweetness and kinship of chords in a key; or when one key passes by modulation to another key; and that through all the chords and all the keys. We shall see wondrously more of this when we come to the study and contemplation of the Chromatic System of Chords. [Scientific Basis and Build of Music, page 112]

The middle portion with the zigzag and perpendicular lines are the chromatic chords, as it were arpeggio'd. They are shown 5-fold, and have their major form from the right side, and their minor form from the left. In the column on the right they are seen in resolution, in their primary and fullest manner, with the 12 minors. The reason why there are 13 scales, though called the 12, is that F# is one scale and G? another on the major side; and D# and E? separated the same way on the minor side. Twelve, however, is the natural number for the mathematical scales as well as the tempered ones. But as the mathematical scales roll on in cycles, F# is mathematically the first of a new cycle, and all the notes of the scale of F# are a comma and the apotome minor higher than G?. And so also it is on the minor side, D# is a comma and the apotome higher than E?. These two thirteenth keys are therefore simply a repetition of the two first; a fourteenth would be a repetition of the second; and so on all through till a second cycle of twelve would be completed; and the thirteenth to it would be just the first of a third cycle a comma and the apotome minor higher than the second, and so on ad infinitum. In the tempered scales F# and G? on the major side are made one; and D# and E? on the minor side the same; and the circle of the twelve is closed. This is the explanation of the thirteen in any of the plates being called twelve. The perpendicular lines join identical notes with diverse names. The zigzag lines thread the rising Fifths which constitute the chromatic chords under diverse names, and these chords are then seen in stave-notation, or the major and minor sides opposites. The system of the Secondary and Tertiary manner of resolution might be shown in the same way, thus exhibiting 72 resolutions into Tonic chords. But the Chromatic chord can also be used to resolve to the Subdominant and Dominant chords of each of these 24 keys, which will exhibit 48 more chromatic resolutions; and resolving into the 48 chords in the primary, secondary, and tertiary manners, will make 144 resolutions, which with 72 above make 216 resolutions. These have been worked out by our author in the Common Notation, in a variety of positions and inversions, and may be published, perhaps, in a second edition of this work, or in a practical work by themselves. [Scientific Basis and Build of Music, page 115]

In the three open columns are the three chromatic chords. In the close columns are the same chromatic chords, with the same designations, on the left. The middle row of letters are the chords of the major keys; the letter with the figure being the key note. The right hand row of letters are the chords of the minor keys marked in the same way. The artist will have no difficulty in making use of the other resolutions of this abundant store; but the young student should make similar tables of the other manners of resolution; he will find abundant help for this in other parts of this work. [Scientific Basis and Build of Music, page 119]

Fig. 3 illustrates the way Nature teaches us by example how to compound so as to enable chords that are separated by the intervention of others to pass to each other. In the middle of the chord scale Nature gives the root of the one chord to the top of the other, and the top of the one to the root of the other; in compounding we are taught by this example to do the same, and the top of the separated dominant is given to the root of the [Scientific Basis and Build of Music, page 120]

Fig. 4 is a setting of the minor and the major chord-scales, showing how they stand linked by notes in common in their direct sequence from dominant minor to dominant major. To each of the six chords is placed the first chromatic chord, showing how it resolves in its three-fold manner by 1, 2, and 3 semitonic progressions in each mode, and by 1 and 2 notes in common variously in each mode; and here again the law of duality is seen in its always symmetrical adjustments. Duality, when once clearly and familiarly come into possession of musicians, will be sure to become an operative rule and test-agent in composition. [Scientific Basis and Build of Music, page 121]

The curved lines enclose the three chords of the major mode of the scale, with the ratio-numbers for the vibration in their simplest expression, counted, in the usual way in this work, from F1, the root of the major subdominant. The chords stand in their genetic position of F F C A, that is F1 by 2, 3, and 5; and so with the other two. The proportions for a set of ten pendulums are then placed in file with the ten notes from 1 to 1/2025 part of 1. Of course the one may be any length to begin with, but the proportions rule the scale after that. [Scientific Basis and Build of Music, page 121]

---

Hughes
The chords
—The fourteen roots of the chords of the twelve major keys
—A threefold major chord examined, fourfold with its octave
—The seven of each key seen to have two chords and its scale one chord, thirty-six in all, forty-eight with octaves
—The chords of the twelve keys as they follow in order are written in musical clef
—Colours seen to agree, . . . 27 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]

The twelve keys, their trinities, scales, and chords, rising seven times through seven octaves, each thirteenth note octave of the previous twelve and first of the rising twelve
—Descending, ascending reversed
—Keys mingled
—The Pendulograph alluded to, . . . 28 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]

The modulating gamut
—One series of the twelve keys meeting by fifths through seven octaves
—Keys not mingled
—A table of the key-notes and their trinities thus meeting
—The fourths not isolated
—The table of the twelve scales meeting by fifths
—The twelve keys, trinities, scales, and chords thus meeting are written in musical clef
—The twelve meeting through seven circles, each circle representing the eighteen tones
—The keys of C and G meeting, coloured
—Retrospection of the various major developments, . . . . 29 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]

The twelve keys, trinities, scales, and chords are written in musical clef,..38 [Harmonies of Tones and Colours, Table of Contents3 - Harmonies]

study of the natural sciences, as we progress, we find that "hills peep o'er hills, and alps o'er alps arise." As regards keyed instruments, it appears that the effect of those notes which act two parts, such as C# and D?, is rectified in some way so as to be perfectly attuned to the ideal of harmony within us. Again, the "Amen" sung by the choir in a cathedral may not be in accurate tune, but if nearly the correct intonation is sounded, after traveling along the aisles, the chords always return to the ear in perfect harmony, because the natural laws of music, assisted by the echoing power of the building, have attuned them to the perfect harmonical triad. If the "Amen" be too much out of tune, these laws decline to interfere, and there is no such helpful resonance.* [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies2, page 16]

combinations of dissonance, rests, sounding neither scale nor chords. Dissonance does not express opposition or separation, for there is no principle in musical tones which is productive of contraries; the dissonances follow the attraction of the tonic, or key-note, and the neutralization of the musical disturbance is implied in the disagreement in their motion with the repose of the unit, or key-note. So far is this from producing separation, that the apparent discord is simply a preparation for growth, the life of harmony causing an inherent tendency towards closer union. [Harmonies of Tones and Colours, Combinations of dissonance, rests, page 24]

The roots of the chords are first written. The Key-note C and its trinities are shewn to have 2 chords. The chords of the 12 Major Keys, as they follow in order. [Harmonies of Tones and Colours, The Roots of the Chords, page 26c]

[Harmonies of Tones and Colours, Diagram V - The Chords of the Twelve Major Keys, page 27a]

If the chords of the twelve keys and the thirteenth octave are struck, all agree in their method of development. We see here the order in which the chords are repeated, and the working of the double tones. As an example of the latter, we may trace the chords belonging to the key of D?, and compare them with those belonging to the key of F#, also the first chord in the key of A?. The fourth note in depth, sounded last of the seven of each harmony, has been seen as preparing for the chords; it prepares equally for the scale, and the scale for the chords, the octave chord of the scale, ascending, preparing for the latter to descend. Descending is ascending reversed. [Harmonies of Tones and Colours, Diagram V - The Chords of the Twelve Major Keys, page 27a]

IF we strike the twelve keys of harmonies in trinities, scales, and chords, as written in musical clef, beginning with the lowest C in the bass clef, this first development is linked into the lower series of seven octaves by the four lower tones sounded by C. If we follow with the twelve keys six times, at the seventh time they will gradually rise into the higher series. We obtain a glimpse of the beauty arising from musical notes in the Pendulograph. How exquisite would they be if they could be represented in their natural coloured tones! — as, for instance, the chord of the scale of C in red, yellow, and blue, with the six coloured tones rising from each, and harmoniously blended into each other. [Harmonies of Tones and Colours, The Twelve Keys Rising Seven Times, page 28a]

The 12 Key-notes and their trinities and scales written in musical clef, with their chords added, all rising in the two octaves, as before. [Harmonies of Tones and Colours, The 12 Keynotes and Their Trinities and Scales, page 28c]

The keys of C and G meeting are coloured, and show the beautiful results of colours arising from gradual progression when meeting by fifths. Each key-note and its trinities have been traced as complete in itself, and all knit into each other, the seven of each rising a tone and developing seven times through seven octaves, the keys mingled. The twelve scales have been traced, developing seven times through seven octaves, all knit into each other and into the key-notes and their trinities. The chords have also been traced, each complete in itself, and all knit into each other and into the key-notes, trinities, and scales. And lastly, one series of the twelve keys, no longer mingled, but modulating into each other, have been traced, closely linked into each other by fifths through seven octaves, three keys always meeting. Mark the number of notes thus linked together, and endeavour to imagine this number of tones meeting from the various notes. [Harmonies of Tones and Colours, The Twelve Scales Meeting by Fifths, page 31a]

THE term "key" in the minor developments must be taken in the sense in which it is understood by musicians, although it will be seen that it is only the seven of the harmony that are the relative minor keys of the majors, the scales with their chords sounding other keys. The grandeur, combined with simplicity, of the laws which develope musical harmonies are strikingly exhibited in the minor keys. Although at first they appear most paradoxical, and, comparing them with the majors, we may almost say contradictory in their laws of development, when they are in some degree understood, the intricacies disappear, and the twelve keys follow each other (with the thirteenth octave), all exactly agreeing in their mode of development. I shall endeavour to trace them as much as possible in the same manner as the majors, the lowest developments of the minor keys being notes with scales and chords, the notes always sounding their major harmonies in tones. Here an apparently paradoxical question arises. If the major keys are gained by the notes sounding the major tones, how are the minor keys obtained? Strictly speaking, there are no minor key-notes: the development of a minor harmony is but a mode of succession within the octave, caused by each minor key-note employing the sharps or flats of the fourth major key-note higher; and with this essential difference, it will be seen in how many points the developments of major and minor harmonics agree. I have carefully followed the same laws, and if any capable mind examines the results, I am prepared for severe criticism. I can only express that it was impossible to gain any other results than the seven of the harmony, the ascending and the descending scale and the chords combining three different keys. [Harmonies of Tones and Colours, Diagram VIII - On the Development of the Twelve Minor Harmonies, page 32]

[Harmonies of Tones and Colours, Diagram XIII - The Twelve Keynotes with Their Trinities, page 38a]

IF we strike the twelve as written in musical clef, beginning with the lowest A in the bass clef, each key-note, with its trinities, scale, and chords, sounds three harmonics. We may follow with the twelve keys as they rise, and descend by following the keys upwards as written in musical clef, each key falling lower. [Harmonies of Tones and Colours, Diagram XIII - The Twelve Keynotes with Their Trinities, page 38a]

The twelve key-notes with their Trinities and Scales repeated, with the addition of the chords. [Harmonies of Tones and Colours, The Twelve Keynotes with Their Trinities and Scales Repeated, page 38c]

BEGINNING with the lowest A in the bass clef, let us strike the trinities, scale, and chords, carrying each key-note a fifth higher, counting the seven belonging to its harmony. If the silent notes are included, each fifth is the eighth meeting. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths1, page 39]

The chords always agree in their harmonies, and thus the close union of all is seen. The corresponding harmonies of tones and colours are also shown. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]

"All things are touched with melancholy,
Born of the secret soul's mistrust
To feel her fair ethereal wings
Weighed down with vile degraded dust.
There is no music in the life
That sounds with idiot laughter solely;
There's not a string attuned to mirth,
But has its chord in melancholy."
Thomas Hood. [Harmonies of Tones and Colours, Reflections on the Scheme3, page 45]

"All theory must be founded on one great fact—harmony; for harmony is the chief beauty of two or more sounds heard together. There may be figure, schemata, and all other niceties of succession and combination; but if no harmony, the music is not beautiful. It is dim, dull, and disagreeable." [Harmonies of Tones and Colours, Fragments from the Last Note-book, page 50]

DIAGRAM XVII.—The roots of the minor chords—The difference between a major and a minor chord—The chords of the 12 minor keys follow. [Harmonies of Tones and Colours, Additional Diagrams, page 57]

DIAGRAM XVIII.—The 12 key-notes with their trinities and scales repeated, with the addition of the chords. [Harmonies of Tones and Colours, Additional Diagrams, page 57]

The student may refer to Diagram XII., where he will find the chords coloured. [Harmonies of Tones and Colours, The Roots of the Minor Chords, page 61]

Remark the three-fold chord of the Trinity, the highest note is the key-note; and in the three-fold chord of the Scale, the key-note is the lowest note. These are the only two chords in each Minor key. [Harmonies of Tones and Colours, The Roots of the Minor Chords, page 61]

---

Cayce
Chord of Life "These as they make for the raising of that from within of the Creative Forces, as it arises along that which is set within the inner man as that cord (chord) of life that once severed may separate, does separate, that balance between the mind, the body, the soul; these three, as accorded within the human forces, are the activities that were carried on by thy self in movement of body in its every motion that made for the uplifting up, the intoning in of self within; that there might come, as it were, the sound as of many waters; or as the morning stars in their circuit about the earth may sing with the glorious coming of the light into the experience of man to raise same to his at-oneness and his attunement with those beauties of the coming of the sons of men into the earth that God in His Oneness of Purpose may bring those activities with the sons of God as an at-onement in their purposes in the earth. The glorifying of Him in the dealings and associations with the fellow man, and these find their attunement in each chord as it rings one with another in all the music that may be heard from every sound that follows in eeiu-u-u-ummmm in its forms, through that attunement along the pineal to the source of light within the self to make for the emotions of glorifying alone." Cayce (275-43)

"For the experience becomes rather as a very delicate instrument of music upon which the chords of life (which is God) are played." Cayce (1436-2)

See Also

---

(BDF chord))
chord types
common root of three chords
compound chord
Degree of Harmonicity
Figure 1.1 - Chord Signatures of Brain Convolutions
Harmonicity
Harmony
Interval
Lost Chord a poem
Major
major chord
Minor
minor chord
Monochord
mors janua vitae
octave chord
Signature
Tetrachord
three mathematical primes
Tone
Triad
Triplet
Waveform
8.21 - Signature same as Chord