Intervals, scales, keys, and chords having intervals a semitone less than major.
John Stainer
Less, smaller. (1) intervals are said to be minor when they contain one semitone less than major. (2) A scale is said to be in the minor mode when its third and sixth are minor. Formerly minor music was described as "with the lesser third." (3) Flute minor, Klein flute, s small flute-stop on the organ, or 4 ft. or 2 ft pitch. [Stainer, John; Barrett, W.A.; A Dictionary of Musical Terms; Novello, Ewer and Co., London, pre-1900]
Ramsay
MINOR - In music a system derived from certain primes in ratios descending. The Scientific Basis and Build of Music
"Of these three chords, which constitute a scale or key, Nature next proceeds to generate, in a similar way, a family of scales or keys, and these in two lines, the Major and the Minor. The twice twelve-fold family of keys is brought forth in much the same way as were the chords which constitute them, and as were the notes which constitute the chords. There is a beautiful growth-like continuity in the production of all." [Scientific Basis and Build of Music, page 20]
In order to find the notes for the next major key above C, we have to multiply the vibration-number of D, which is the top of the dominant C, by 3 and 5. It is out of the key of C at this point that the new key sprouts and grows, and by the primes and method which produce the key of C itself. So if we would find the relative minor of C, let us take the note which is a minor third below D - that is, B - to produce the minor. The minor sprouts and grows from this point of the key of C; for the relative minor grows out of the major, as out of the man at first the woman is taken. Moreover, B is the last-born of the notes for the major scale; for the middles, that is, the thirds of chords, are always produced by the prime 5; and the tops, that is, the fifths of chords, are produced by the prime 3, and are born before the thirds, though placed after them in the chords. Well, because B is the last-born note of the major, as well as a minor third below the top of the highest chord of the major, it seems that the minor should have this for its point of departure. Again, we have seen that the major and the minor are found in their strings and their vibrations by an inverse process, that one going back upon the other; and, there taking Nature's clue, let us proceed by an inverse process of generating the minor. Making B45 our unit, as F1 was our unit for the major, let us divide by 3 and 5 for a root and middle to B, as we multiplied by 3 and 5 for a top and middle to F. B45 divided by 3 is 15; here then is our E, the root of the chord, just where we had found it coming upward; for, remember, we found E15 by multiplying C3 by 5. This E, then, is the same in major and minor. Now B45 divided by 5 is 9; [Scientific Basis and Build of Music, page 31]
this is the middle of our chord, E, G, B; and remember that this also is G as we found it coming upward, C3 multiplied by 3 being G9. This is another note of the minor, the same in its quantity as that of the major. Now for another chord downward we must divide the root of the one we have found, namely E15, by 3, which will give us A5, the root of a center chord for the minor, and the very key-note of the relative minor to C. And remember that this A5 is just as we found it in coming upward, for F multiplied by 5 gave us A5. Now divide E15 by 5 and we have C3, the middle to our minor chord, A, C, E. Still we must remember that this C3 is just as we found it coming upward, for F multiplied by 3 is C3. Behold how thus far major and minor, though inversely developed, are identically the same in their notes, though not in the order in which they stand in the fifths thus generated. [Scientific Basis and Build of Music, page 32]
The number 3 is the creative power in music, producing fifths, but it is under the control of the Octave prime - the number 2. It is the supreme octave which forms a boundary by making twelve fifths and seven octaves unite in one note. Within this horizon lies the musical system in its threefoldness - major, minor, and chromatic. [Scientific Basis and Build of Music, page 35]
There are joinings, however, though at a wilder limit. The system of music is not a spiral line. The minor scale is developed from the major by the law of Duality; and when this is done, D26 2/3, the root of the subdominant minor, is so near to D27, the top of the dominant major, that one note may be made to serve for both; and this joins the one extreme of the major and minor systems in this note D, which has thus duality in itself. The only other place where the dual system of major and minor stands open is at the other extreme of the two modes, between B, the top of the dominant minor, and F the root of the subdominant major; and these unjoined ends reach away till at three fifths below F, namely A?, and at three fifths above [Scientific Basis and Build of Music, page 38]
It runs in all the polarities of Nature. Music, as belonging to Nature - as one of the things which the Great Numberer hath created - is under this Law of Duality as well as that of mathematical ratios and other laws. The Law of Duality in music gives the major and minor systems. As the major is derived from certain primes in ratios ascending, and the minor from the same primes in the same ratios descending, they are inversely related; and these diatonic scales have in the responding parts exactly the same quantities. But as multiplying by 3 three times gives the framework of the major system in the ascending Genesis, and dividing by 3 three times gives the framework of the minor system in the descending Genesis. They are in this view also directly related. The Law of Duality in music emerges into view from the Genesis [Scientific Basis and Build of Music, page 42]
of the major being upward, and the Genesis of the minor being downward. The ascending Genesis, beginning with the root of the subdominant major F, produces in the ascent a scale of notes at varying distances, and of increasing levities; the middle note, D27, being carried a little above the center of the system. The descending Genesis, beginning with the top of the dominant minor B, produces in the descent a scale of notes with identical variety of distances, but with increasing gravities; the middle note, D26 2/3, being pressed a little below the center of the system, thus giving rise to these two D's - one whose genetic number is 27, the major D, and one whose genetic number is 27 2/3, the minor D - the duality of D is thus residing in itself.1 [Scientific Basis and Build of Music, page 43]
It is in their inverse relations that the major and the minor are equal. Every note, chord, and progression in the one has its reciprocal or corresponding note, chord, and progression in the other. This is the Law of Duality. And this general law of Nature is so deeply rooted in music, that is the numbers which represent the vibrations in the major system be made to represent quantities of string, these quantities will produce the minor system (beginning, of course, with the proper notes and numbers); so that when the quantities are minor the tones are major, and when the quantities are major the tones are minor.1[Scientific Basis and Build of Music, page 44]
among the Greeks on account of having symmetry in itself. The primitive scale was doubtless that which is the model of all major music; and our minor model is its dual, as Ramsay has shown, which in its Genesis indicates the duality of all the rest of the notes, although it is not probable that the Greeks saw the musical elements in this light. It is remarkable and significant that in their modes the Greeks did not lift up the scale of Nature into different pitches, preserving its model form as we do in our twelve major scales, but keeping the model form at one pitch they built up their symmetrical tetrachords, allowing the larger and lesser tones of the primitive scale to arrange themselves in every variety of place, as we have shown in the table of tetrachord modes above. Without seeing the genetic origin of music's duality they were led to arrange the modes by symmetry, which is one of the phases of duality. Symmetry is duality in practice. It may not always be apparent how symmetry originates in Nature; but in music, the art of the ear, duality emerges in the Genesis of the minor scale; in the true mathematical build of the major on the root of the major subdominant F, and the true relation of the minor to it in the inverse genesis descending from the top of the minor dominant B. [Scientific Basis and Build of Music, page 46]
Nature has not finished when she has given us the Diatonic Scale of notes as first generated. In the diatonic scale, in ascending from C, the root of the tonic, the first step is an interval of 9 commas, supposing that we adopt the common division of the octave into 53 commas, which is the nearest practical measuring rule; the second step has 8 commas; the third has 5; the fourth has 9; the fifth has 8; the sixth has 9; and the seventh and last has 5 commas. So we have three steps of 9 commas, two steps of 8, and two of 5. The order of the steps in the major is 9, 8, 5, 9, 8, 9, 5. In the minor the magnitudes are the same, but the order is 9, 5, 8, 9, 5, 9, 8. So there are three magnitudes.1 But Nature has an equalizing process in the course of her musical marshallings, in which these greater ones get cut down, and have to change places with the lesser, when her purpose requires them so to do. [Scientific Basis and Build of Music, page 47]
There are two Diatonic systems in Music - the major and the minor. With the exception of one note, all the notes of the one system are identical with those of the other. The major key C has all the notes of the minor key A excepting D, the root of the minor subdominant; and the minor has all the notes of the major exception D, the top of the major dominant. These twain are one music, the masculine and feminine of a twofold unity; one system in duality rather than two systems. [Scientific Basis and Build of Music, page 50]
There are two semitones in each system, B-C and E-F. But when the notes of the two systems are being generated simultaneously, the two semitonic intervals originate separately. While the major is generating the semitone E-F, the third and fourth of the major scale, the minor is generating the semitone B-C, the second and third of the minor scale. So E-F is the semitone which belongs genetically to the major, and B-C to the minor.1 These two semitones are the two roots of
THE CHROMATIC SYSTEM,
and they are found together in what has been called the "Minor Triad," and by other names, namely, B-D-F. [Scientific Basis and Build of Music, page 50]
In going round the circuit of the common chords of the major and its relative minor, and beginning our circuit with the minor, we encounter a triplet,2 differing from all the rest in its constituents, thus -
Here we have passed through minor and major from D to D, and seem to have come to the point from which we started; but we know that these two D's are [Scientific Basis and Build of Music, page 53]
not mathematically identical, the genetic number of the last D, the top of the dominant major, being 27, and that of the first D, the root of the subdominant minor, being 26 2/3. Well, in the triplets of the minor we have minor thirds below their middles, D-F, A-C, E-G. In the triplets of the major we have minor thirds above their middles, A-C, E-G, B-D. But here between the triplets of the two modes we have a triplet which has minor third both below and above its middle note, two minor thirds and nothing else, B-D-F. Here, then, the Diatonic progression chords presents us with a 3-note Chromatic chord, and marchals us the way that we must go to find [Scientific Basis and Build of Music, page 54]
But, as the subdominant sixth and dominant seventh suggest that the chromatic chord should be a 4-note chord, we must find out how Nature completes this diatonic chromatic triad and makes it a 4-note chord, and that according to its own intrinsic character as of minor thirds. Nature has always a rationale in her operations which it is ever delightful to discover. Wedged in between the minor dominant and the major subdominant, this triad, B D F, has already B, the top of the dominant minor, for its root; and F, the root of the subdominant major, for its top; and its middle is the mysterious D which, in its two positions as root of the minor subdominant and top of the major dominant, stands at the two extremes of the whole twofold diatonic key, bounding and embracing all; and which in its two degrees as D26 2/3 and D27 claims kindred with both minor and major modes of the twofold key system. Surely this Janus-faced D, looking this way toward the minor and that way to the major, seems to say, "the complement of this chord, of which I am the heart, is not far to seek nor hard to find on either side." It has already B in common with the minor dominant; the very next step is to the middle of this chord, G. Roots and tops of chords may not be altered, but middles may with impunity be flattened or sharpened as occasion may require. No two of them in succession in the chord-scale have the same structure; the chromatic triad, in claiming this middle, claims it sharpened, for it must have [Scientific Basis and Build of Music, page 54]
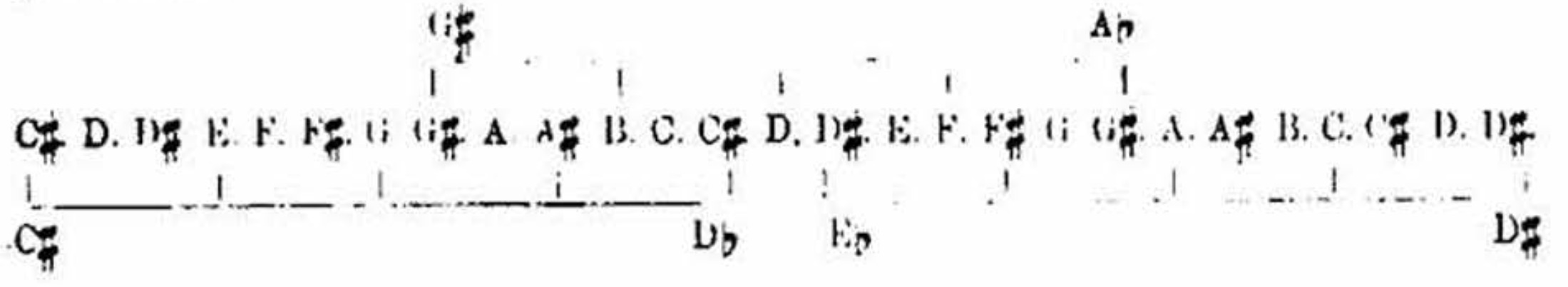
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
By taking four minor thirds upward from G# or downward from A?, we have the first chromatic chord in its twofold form. Its central note is D, the top of the dominant major, and the root of the subdominant minor, being its own dual, that is to say, its minor birth being dual to its major birth.1 On the keyboard it has the same order of keys above it and below it; this dual D [Scientific Basis and Build of Music, page 56]
lastly it is altered again and becomes, by the power of 3 once more, F#,#, and serves in four keys. But this carries us beyond the horizon of our musical world of twelve keys; for in B#, the top of the tonic E, we have reached our twelfth fifth, and it here coalesces with C of the seventh octave, and closes the circle. This is the way that all notes become alternately altered, either by commas and sharps in the upward genesis of scales, or by commas and flats in the downward Genesis, by the alternate powers of 3 and 5. In the upward Genesis in this illustration, notes by the power of 5 serve in three keys, and those by the power of 3 serve in four keys. In the minors it is just the inverse on this by the Law of Duality. But no note serves for more than either three or four keys, as the case may be. [Scientific Basis and Build of Music, page 63]
embedded; and in the minor tonic chord A C E in the same way is embedded its own semitone; and in these chords they appear in their proper places as third and fourth, C, d, E f, G; and second and third, A, b C, d, E. It is these first five notes of the octave scale which in a very distinctive way constitute the natural scale, which can be harmonized consecutively in one manner. The octave is seen in this view to be a compound scale, inasmuch as a compounding method of harmonizing has to be resorted to in passing consecutively from the sixth to the seventh. Similar compounding has to be done in the minor as well.1 [Scientific Basis and Build of Music, page 65]
Moreover, it is only from one to five, that is from C to G in ascending, which is its proper direction in the Genesis, that the major in being harmonized does not admit of minor chords, but if we descend this same natural major scale of the fifth from five to one, that is from G to C, the first chord is C E G; the next chord is F A C; if this is succeeded by the minor chord A C E, there are two notes in common and one semitonic progression, as very facile step in harmony; and the following two notes are most naturally harmonized as minor chords. So modulation into the minor, even in this major scale, is very easy in descending, which is the proper direction of the minor genesis.2 In a similar way, it is only from five to one, that is from E to A in descending, which is its proper genetic direction, that the minor in being harmonized does not admit of major chords; but if we ascend this same minor scale of the fifth from one to five, the first chord is A C E, the next is E G B, and if this chord be followed by the major C E G, there are here again two notes in common and one semitonic progression; and the two notes following are then most naturally harmonized as major chords. So modulation into the major, even in this minor scale, is very natural and easy in ascending, which is the proper direction of the major genesis.3 The dominant minor and the tonic major are, like the subdominant major and the tonic minor, very intimately related in having two notes in common and one semitonic progression. [Scientific Basis and Build of Music, page 65]
The great Genetic Scale, major and minor, the seed-bed and nursery of all, is that from which first of all the natural scale of the fifth arises into existence; and three fifths are generated in the major ascending side and three also in the descending minor side of the twofold Genesis, giving us six fifths in all. At the top of the ascending genesis we find the major octave scale standing solid and in its perfect order and proportion; and at the bottom of the descending genesis we have the minor octave. [Scientific Basis and Build of Music, page 66]
This great genetic scale, the all-producer, the all-container, extends over six octaves on each side; for it is not till high in the sixth octave we get B in the major, and it is not till low in the sixth octave that we get F in the minor. It is in the fifth octave, however, that the note which is the distinctive mark of the masculine and feminine modes is generated. D27 in the major, and D26 2/3 in the minor, distinguishes the sex of the modes, and shows which is the head and which the helpmeet in this happy family.2 On the major side F, the root of the subdominant chord, that is the chord which is a fifth below the key-note C, is the root of all. This is the beginning of this creation. If we call the vibration-number of F one, for simplicity's sake, then F1 is multiplied by 3 and by 5, which natural process begets its fifth, C, and its third, A; this is the root, top, and middle of the first chord. From this top, C3, grows the next chord by the same natural process, multiplying by 3 and by 5; thus are produced the fifth and third of the second chord, G and E. From the top of this second chord grows the third and last chord, by the repetition of the same natural process; multiplying G9 by 3 and by 5 we [Scientific Basis and Build of Music, page 66]
Now we come to a remarkable arrangement of Nature. The minor does not grow in the same way out of this third chord's top. Two features come before us: first the minor chord grows out of the major, but it is taken not from the top but from the middle, from a rib out of his side. B, the middle of the major dominant chord; B, the last-born of the major genesis; B is the point of departure in the outgrowth of the minor mode. The feminine is a lateral growth from the masculine. Another feature: it grows downward, like a drooping ash or willow. Its first generated chord is its dominant, and its last is its subdominant. Its middle chord, like the middle one of the major, is its tonic. Still further, it is generated by division, not multiplication; B45 is divided by 3 and by 5 for the root and middle of this highest chord, E and G. E15 is divided by 3 and 5 for the root and middle of the tonic chord, A and C. A5 is divided by 3 and 5 for the root and middle of the lowest chord, D and F. Thus we have the whole generation of the elements of music, six generations of harmony, like the six days of creation. Up to this point the whole process and aspect is inverse; growing from a middle; growing downward; growing by division;- while the major is growing from the top; growing upward; growing by multiplication. But here the inverse aspect ends. The generating primes of the major are 3 and 5; 3 and 5 are also the generating primes of the minor. In this essential phase of their creation their comparison is direct, not inverse. [Scientific Basis and Build of Music, page 67]
At the extremes of these two operations we find D the top of the major dominant, and D the root of the minor subdominant; and while all the other notes, whether produced by multiplication of the major roots or division of the minor tops, are the same in their ratio-numbers, the two D's, by no speciality of production, are nevertheless specifically diverse by one comma in their vibration-number, and make a corresponding diversity in the intervals of the two modes. These, the Ray and Rah of the Sol Fa expression, originate a very interesting and somewhat mysterious feature in this great twofold genetic scale. [Scientific Basis and Build of Music, page 67]
Music, and mathematics have nothing more to do with it. Already the Law of Position has guided the Genesis upward in the major; and while mathematical primes were generating the chords one after another in precisely the same way and form, like peas in a pod, the Law of Position was arranging them one over the other, and so appointing them in their relative position each its own peculiar musical effect bright and brighter. And when the major had been thus evolved and arranged by ratios and position, another law, the Law of Duality, gave the mathematical operation its downward direction in the minor; and while the primes which measured the upward fifths of the major also measure the downward fifths of the minor, the Law of Position is placing them in their relative position, and appointing each its own peculiar effect grave and graver. [Scientific Basis and Build of Music, page 68]
The peculiar effects are exhibited when the chord-scale is next set forth. We have seen that there are six chords evolved in the Genesis upward and downward, 3 in the major form and 3 in the minor. In the fifths of the minor the semitone is always in the lower third, occurring between the second and third in the subdominant and tonic, and between the first and second in the dominant chord; whereas in the major it is always in the upper third, between the fourth and fifth in the subdominant, and between the third and fourth in the tonic and dominant chords. While the thirds which the fifths contain are thus so varied, the fifths themselves have always one magnitude, whether major or minor. [Scientific Basis and Build of Music, page 68]
The chord-scales may be either major or minor, or may be found in a sweetly mingled condition; a piece may be wholly major or wholly minor, but not wholly chromatic. Chromatic chords do not usually succeed each other, but come into diatonic compositions for the purpose of producing certain effects peculiar to them, or by solving difficulties which may arise in composition. They are used as musical condiments to spice or sweeten a passage; but nobody makes pudding all of spice or sugar. The structure, character, and progression of the various chord-scales will be found so amply set forth in several parts of this work that it is not necessary to enlarge further in this place. [Scientific Basis and Build of Music, page 69]
The Chromatic Scale is naturally the last to come into view, for it is not generated by a mathematical process at all. Chromatic intervals are indeed found in the scale as mathematically generated. The semitones between B-C and E-F are two chromatic intervals, and the chord which occurs between the major and the minor in the chord-scale when it begins with the minor mode is a chromatic chord, though in an uncompleted condition. But the making of the octave into a chromatic scale of twelve small or semi-tones, is the work of modulation from one key to another through the whole twelve keys in either the major or minor sphere; and this process is fully set forth in the pre-note to the chromatic treatise. [Scientific Basis and Build of Music, page 69]
The number of Diatonic Chords. In the major there are three simple chords, two compound chords, and two double compound, seven in all - subdominant, tonic, dominant, subdominant sixth, subdominant fourth, dominant seventh, and dominant ninth. In the minor there are the same number and order, making fourteen. It is not normal to the tonic chord to compound, but it may, in exceptional instances; the major tonic may, in a certain cadence, assume the top of the minor subdominant; and the minor tonic may assume, in a cognate case, the root of the major dominant.1 [Scientific Basis and Build of Music, page 70]
less variety of effect than we find in the diatonic chords; for although these chords may appear with their notes diversely named, there are still only the three. On account of their cosmopolitan character they need, and they have, no compounding with anything else. They are themselves at home everywhere; like a universal joint, they can turn any way, and affiliate in all directions. Being 4-note chords, and all of minor thirds, their effect is always minor, and they fall with loving softness to the diatonic chords to which they resolve. How this chord in its germ is found in the diatonic chord-scale; how it becomes a 4-note chord of minor thirds; how it variously resolves, each one of the three, in three manners with 24 tonic chords - all this is so fully set forth in the pre-note and treatise on the chromatic chord that it need not be more discussed in this place. See also Plates XVI., XVII., XVIII., XIX., and XX. [Scientific Basis and Build of Music, page 73]
There is nothing extraordinary in this. It is another fact which gives this one its importance, and that is that the musical system is composed of three fifths rising one out of another; so this note by 3/4 becomes the root not only of a chord, but the root of all the three chords, of which the middle one is the tonic; the chord of the balance of the system, the chord of the key; the one out of which it grows, and the one which grows out of it, being like the scales which sway on this central balance-beam. Thus F takes its place, C in the center, and G above. These are the 3 fifths of the system on its masculine or major side. The fractions for A, E, and B, the middle notes of the three chords, are 4/5, 3/5, and 8/15; this too tells a tale; 5 is a new ingredient; and as 3 gives fifths, 5 gives thirds. From these two primes, 3 and 5, along with the integer or unit, all the notes of the system are evolved, the octaves of all being always found by 2. When the whole system has been evolved, the numbers which are the lengths of the strings in the masculine or major mode are the numbers of the vibrations of the notes of the feminine or minor mode; and the string-length-numbers of the minor or feminine are the vibration-numbers of the notes of the major or masculine mode. These two numbers, the one for lengths and one for vibrations, when multiplied into each other, make in every case 720; the octave of 360, the number of the degrees of the circle. [Scientific Basis and Build of Music, page 76]
At the first, in the laws of quantities and motions adjusting musical vibrations, there is one chord of the three notes, F, A, C, the root, middle, and top of the five notes which compose the true natural scale; this one chord can be reproduced a fifth higher, C, E, G, in the same mathematical form, taking the top of the first for the root of the second chord. In like manner this second can be reproduced another fifth higher, G, B, D, still in the same mathematical form, and so fit to be a member of the chord-scale of a key. But the law does not admit of another reproduction without interfering with the first chord, so that a fourth fifth produces no new effect; but the whole key is simply a fifth higher, i.e., if the fourth fifth has been properly produced by multiplying the top of the third fifth by 3 and by 5, the generating primes in music. That this carries us into a new scale is seen in that the F is no longer the F? but F#, and the A is no longer A? but A,. But if we suppose the fourth fifth to be simply the old notes with their own vibration numbers, then D, F, A would not be a fifth belonging either to the major or the minor mode, but a fifth a comma less. The letters of it would read like the minor subdominant, D, F, A; but the intervals, as found in the upward development of the major genesis, instead of being, when expressed in commas, 9, 5, 8, 9, which is the minor subdominant, would be 8, 5, 9, 8, which is not a fifth of the musical system; these having always, whether major or minor, two 9's, one [Scientific Basis and Build of Music, page 77]
In compound chords there are no new notes created; they are found by combining the notes of the simple chords. The dominant sevenths, major and minor, are compounded by adding one from the subdominant. [Scientific Basis and Build of Music, page 79]
G# as it occurs in the scales of A, E, and B major, and A? as it occurs in the scales of F and B? minor, are only distant the apotome minor, and are well represented by one key of the piano. It is only G# as it occurs in the scale of F six sharps major, and A? as it occurs in the scale of E six flats minor, that is not represented on the piano. These two extreme notes F# and E? minor are at the distance of fifteenth fifths and a minor third from each other. This supplies notes for 13 major and 13 minor mathematical scales; but as this is not required for our musical world of twelve scales, so these far-distant G# and A? are not required. The piano is only responsible for the amount of tempering which twelve fifths require, and that is never more than one comma and the apotome minor. [Scientific Basis and Build of Music, page 80]
Having found the framework of the major scale by multiplying F1 three times by 3, find the framework of the minor by dividing three times by 3. But what shall we divide? Well, F1 is the unbegotten of the 25 notes of the great genetic scale; B45 is the last-born of the same scale. We multiply upward from F1 for the major; divide downward from B45 for the minor. Again, B45 is the middle of the top chord of the major system, a minor third below D, the top of that chord, and the top of the whole major chord-scale, so B is the relative minor to it. Now since the minor is to be seen as the INVERSE of the major, the whole process must be inverse. Divide instead of multiply! Divide from the top chord instead of multiply from the bottom chord. Divide from the top of the minor dominant instead of multiply from the root of the major subdominant. This will give the framework of the minor system, B45/3 = E15/3 = A5/3 = D1 2/3. But as 1 2/3 is not easily compared with D27 of the major, take a higher octave of B and divide from it. Two times B45 is B90, and two times B90 is B180, and two times B180 is B360, the number of the degrees of a circle, and two times B360 is B720; all these are simply octaves of B, and do not in the least alter the character of that note; now B720/3 is = E240/3 = A80/3 = D26 2/3. And now comparing D27 found from F1, and D26 2/3 found from B720, we see that while E240 is the same both ways, and also A80, yet D26 2/3 is a comma lower than D27. This is the note which is the center of the dual system, and it is itself a dual note befittingly. [Scientific Basis and Build of Music, page 81]
If the minors are to be developed by sharps in an ascending series of fifths, then the mathematical process must be, as in the majors, by multiplying the top of the dominant by 3 and by 5, and they will then follow the majors. But the Genesis must first necessarily be produced by the descending process. [Scientific Basis and Build of Music, page 84]
And it is another very interesting fact that those numbers multiplied into each other always make 720, the number in the minor genesis which corresponds to 1 in the major; F1 being the generative root of the major, and B720 the generative top of the minor; so adjusted they place the two D's beside each other - D26 2/3 and D27 - and we see the comma of difference between these two numbers which are distinctive of the major and the minor; 26 2/3 x 3 = 80, and 27 x 3 = 81, and 80:81 is the ratio of the comma. This is the Ray and the Rah in which there lurks one of music's mysteries. Let him that is wise unravel it. It is symbolic of something in the spiritual realm of things; its full meaning is only found there. [Scientific Basis and Build of Music, page 88]
notes each; that is, 24 new notes, which, with the seven original major notes and the one different minor note, make 32 in all; and 32 notes in the Octave are all that belong to 13 major and 13 minor mathematical scales.1 [Scientific Basis and Build of Music, page 89]
The reason why there are 13 mathematical scales is that G? and F# are written separately as two scales, although the one is only a comma and the apotome minor higher than the other, while in the regular succession of scales the one is always 5 notes higher than the other; so this G? is an anomaly among scales, unless viewed as the first of a second cycle of keys, which it really is; and all the notes of all the scales of this second cycle are equally a comma and the apotome higher than the notes of the first cycle; and when followed out we find that a third cycle is raised just as much higher than the second as the second is higher than the first; and what is true of these majors may be simply repeated as to the D# and E? of the minors, and the new cycle so begun, and all successive minor cycles. Twelve and not thirteen is the natural number for the mathematical scales, which go on in a spiral line, as truly as for the tempered scales, which close as a circle at this point. [Scientific Basis and Build of Music, page 89]
It must be noted that the two new notes needed for each new scale are quite a different affair from the sexual note, that is the note which is different in major and minor, e.g., the two D's in major C and minor A. The [Scientific Basis and Build of Music, page 90]
"There are three chromatic chords, and each of these three is related to eight particular tonic chords. When one the these chromatic chords goes to any one of its eight tonic chords, three of its notes move in semitonic progression, and the other note moves by the small tone, the ratio of 9:10. There is exception to this rule, whether the key be major or minor. But when the chromatic chord which should resolve to the tonic of C is followed by the subdominant, or the tonic of F (the example in Mr. Green's book), only two of its notes move in semitonic progress. Your friend describes the chord as if it had gone to the tonic of B; and what he said about it, and about D going to C, is what is supposed to be [Scientific Basis and Build of Music, page 94]
notes attracted by proximity are attracted in the direction of the center of the tonic chord, major or minor. But if D in the major is attracted by C, the root of the tonic, then it would be moving away from the center. Two notes which have the ratio of 8:9, as C and D, or two notes which are produced by the same ratio as C and D, or two notes where each of them is either a root or a top, as C and D, never resolve to each other by proximity. It is an invariable order that one of the notes should be the middle of a chord. [Scientific Basis and Build of Music, page 99]
"What we have thus said about the resolving notes to the major tonic has been allowed in the case of the minor. No one ever said that the second of the minor scale resolved to the root of the tonic. Notwithstanding the importance of the tonic notes, the semitonic interval above the second of the scale decided the matter for the Law of Proximity; and no one ever said that D, the root of the subdominant minor, did not resolve to C, the center of the tonic minor, on the same terms that two notes are brought to the center of the tonic major; with this difference, that the semitonic interval is above the center in the major and below it in the minor. The other two notes which resolve into the tonic minor are on the same terms as the major; with this difference, that the semitonic interval is below the root of the tonic major and above the top of the tonic minor. And the small tone ratio 9:10 is above the top of the tonic major and below the root of the tonic minor. If it has been the case that D resolved to the root of the tonic major, then, according to the Law of Duality, there would have been another place where everything would have been the same, only in the inverse order; but, fortunately for itself, the error has no other error to keep it in countenance. This error has not been fallen into by reasoning from analogy. [Scientific Basis and Build of Music, page 99]
The intervening chord between the Diatonic and Chromatic systems, B, D, F. - This chord, which has suffered expatriation from the society of perfect chords, is nevertheless as perfect in its own place and way as any. From its peculiar relation to both major and minor, and to both diatonic and chromatic things, it is a specially interesting triad. F, which is the genetic root of all, and distinctively the root of major subdominant, has here come to the top by the prime 2. D, here in the middle, is diatonically the top of the major dominant, and the root of the minor subdominant; and on account of its self-duality, the most interesting note of all; begotten in the great Genesis by the prime 3. B, the last-begotten in the diatonic genesis, top of the diatonic minor, middle of the dominant major, and begotten by the prime 5, is here the quasi root of this triad, which in view of all this is a remarkable summation of things. This B, D, F is the mors janua vitae in music, for it is in a manner the death of diatonic chords, being neither a perfect major nor a perfect minor chord; yet it is the birth and life of the chromatic phase of music. In attracting and assimilating to itself the elements by which it becomes a full chromatic chord, it gives the minor dominant the G# which we so often see in use, and never see explained; and it gives the major subdominant a corresponding A?, less frequently used. It is quite clear that this chromatic chord in either its major phase as B, D, F, A?, or its minor phase as G#, B, D, F, is as natural and legitimate in music as anything else; and like the diatonic chords, major and minor, it is one of three, exactly like itself, into which the octave of semitones is perfectly divided. [Scientific Basis and Build of Music, page 101]
In Fig. 1, the mathematical framework of the scales major and minor, is shown the genesis of the scale. F1, in the top figure, is multiplied by 3, and that by 3, and that by 3, which brings us to D27, top of the major dominant. F1 is the root of the whole system. C3 is the top of the first chord, and from that grows the next, and from that the next; and so we have F, C, G, and D, the tops and roots of the major system of chords. When these 3 roots are each multiplied once by 5, the middles of the chords are found, as shown - A, E, and B; so B is the last-born of the major family. When B is taken 4 octaves higher at the number 720 and divided by 3, and that by 3, and that by 3, we get the notes E, A, and D, which are the roots and tops of the minor system of chords. Dividing B, E, and A each by 5 once, we get the middles of the 3 minor chords, as shown. [Scientific Basis and Build of Music, page 103]
In the lowest Fig. this framework is filled up with all the octaves of the notes found as in the top Fig., the major being evolved upward and the minor downward, and the two systems centered at the D's, which are shown a comma distant from each other. [Scientific Basis and Build of Music, page 103]
The middle Fig. is the same, the central D's being made a pivot point on which to turn the minor down against the major in an inverse relation, setting the dual notes in file. The multiplying primes are set over the roots. The arrows point out the notes so found. The two D's are here seen right opposite of each other, because the intervals between C D in the major and E D in the minor are equal. [Scientific Basis and Build of Music, page 103]
This plate is a representation of the area of a scale; the major scale, when viewed with the large hemisphere, lowest; the minor when viewed the reverse way. It is here pictorially shown that major and minor does not mean larger and smaller, for both modes occupy the same area, and have in their structure the same intervals, though standing in a different order. It is this difference in structural arrangement of the intervals which characterizes the one as masculine and the other as feminine, which are much preferable to the major and minor as distinctive names for the two modes. Each scale, in both its modes, has three Fifths - subdominant, tonic, and dominant. The middle fifth is the tonic, and its lowest note the key-note of the scale, or of any composition written in this scale. The 53 commas of the Octave are variously allotted in its seven notes - 3 of them have 9 commas, 2 have 8, and 2 have 5. The area of the scale, however, has much more than the octave; it is two octaves, all save the minor third D-F, and has 93 commas. This is the area alike of masculine and feminine modes. The two modes are here shown as directly related, as we might figuratively say, in their marriage relation. The law of Duality, which always emerges when the two modes are seen in their relationship, is here illustrated, and the dual notes are indicated by oblique lines across the pairs. [Scientific Basis and Build of Music, page 106]
The larger hemisphere of the Fifths is uppermost when taking the minor view of the plate, and suggests the idea of the minor being weighed downward, as it really is mathematically in the genesis of the scale, which is seen in the D of the minor being a comma lower than the D of the major. Taking the major view of the plate, the smaller hemisphere is uppermost, and suggest the idea of rising upward, as it really does in the [Scientific Basis and Build of Music, page 106]
mathematical genesis, as seen in its D being a comma higher than that of the minor. This gravity and buoyancy of the modes is a striking feature of them. In the Thirds it is different from the Fifths; the larger hemisphere of each third seems gravitating toward the center of the tonic chord. The area of the scale has then the aspect of a planet with its north and south poles, and pervaded by a tendency towards the center; the center itself being neutral as to motion. [Scientific Basis and Build of Music, page 107]
The Plate shows the Twelve Major and Minor Scales, with the three chords of their harmony - subdominant, tonic, and dominant; the tonic chord being always the center one. The straight lines of the three squares inside the stave embrace the chords of the major scales, which are read toward the right; e.g., F, C, G - these are the roots of the three chords F A C, C E G, G B D. The tonic chord of the scale of C becomes the subdominant chord of the scale of G, etc., all round. The curved lines of the ellipse embrace the three chords of the successive scales; e.g., D, A, E - these are the roots of the three chords D F A, A C E, E G B. The tonic chord of the scale of A becomes the subdominant of the scale of E, etc., all round. The sixth scale of the Majors may be written B with 5 sharps, and then is followed by F with 6 sharps, and this by C with 7 sharps, and so on all in sharps; and in this case the twelfth key would be E with 11 sharps; but, to simplify the signature, at B we can change the writing into C, this would be followed by G with 6 flats, and then the signature dropping one flat at every new key becomes a simpler expression; and at the twelfth key, instead of E with 11 sharps we have F with only one flat. Similarly, the Minors make a change from sharps to flats; and at the twelfth key, instead of C with 11 sharps we have D with one flat. The young student, for whose help these pictorial illustrations are chiefly prepared, must observe, however, that this is only a matter of musical orthography, and does not practically affect the music itself. When he comes to the study of the mathematical scales, he will be brought in sight of the exact very small difference between this B and C?, or this F# and G?; but meanwhile there is no difference for him. [Scientific Basis and Build of Music, page 108]
In the center column are the notes, named; with the lesser and larger steps of their mathematical evolution marked with commas, sharps, and flats; the comma and flat of the descending evolution placed to the left; the comma and sharp of the ascending evolution to the right; and in both cases as they arise. If a note is first altered by a comma, this mark is placed next to the letter; if first altered by a sharp or flat, these marks are placed next the letter. It will be observed that the sharpened note is always higher a little than the note above it when flattened; A# is higher than ?B; and B is higher than ?C, etc.; thus it is all through the scales; and probably it is also so with a fine voice guided by a true ear; for the natural tendency of sharpened notes is upward, and that of flattened notes downward; the degree of such difference is so small, however, that there has been difference of opinion as to whether the # and ? have a space between them, or whether they overlap, as we have shown they do. In tempered instruments with fixed keys the small disparity is ignored, and one key serves for both. In the double columns right and left of the notes are their mathematical numbers as they arise in the Genesis of the scales. In the seven columns right of the one number-column, and in the six on the left of the other, are the 12 major and their 12 relative minor scales, so arranged that the mathematical number of their notes is always standing in file with their notes. D in A minor is seen as 53 1/3, while the D of C major is 54; this is the comma of difference in the primitive Genesis, and establishes the sexual distinction of major and minor all through. The fourth of the minor is always a comma lower than the second of the major, though having the same name; this note in the development of the scales by flats drops in the minor a comma below the major, and in the development of the scales by sharps ascends in the major a comma above the minor. In the head of the plate the key-notes of the 12 majors, and under them those of their relative minors, are placed over the respective scales extended below. This plate will afford a good deal of teaching to a careful student; and none will readily fail to see beautiful indications of the deep-seated Duality of Major and Minor. [Scientific Basis and Build of Music, page 109]
With perfect duality of response does resolution of chords go on in the minors. When the tonic chord follows the subdominant one, they have for their note in common A, i.e., in the key of A; and the middle of the subdominant moves by semitonic progression to the top of the tonic. When the tonic chord follows the dominant one, the top of the tonic and the root of dominant E is a note in common, and the top of the dominant goes by semitonic progression to the middle of the tonic. These simple chords are thus linked together exactly with the same degree of continuity as the simple chords of the major. When the tonic chord follows the compound subdominant, this compound chord, like the compound dominant in the major, has two semitonic progressions - one to the top and one to the middle of the tonic - and they have one note in common. When the compound dominant follows the subdominant, the root of the subdominant is lent to the top of the dominant, and thus a note in common is created, and the middle of the subdominant moves by semitonic progression to the root of the dominant. When the compound subdominant follows the dominant, the top is lent to the root of the subdominant, creating a note in common between them, and the root of the dominant goes to the middle of the subdominant in semitonic progression. This is the way of Nature. The unbroken continuity of her ways is perfectly illustrated in the linked sweetness and kinship of chords in a key; or when one key passes by modulation to another key; and that through all the chords and all the keys. We shall see wondrously more of this when we come to the study and contemplation of the Chromatic System of Chords. [Scientific Basis and Build of Music, page 112]
When the major and minor scales are generated to be shown the one half in #s and the other half in ?s, it is not necessary to carry the mathematical process through the whole 24, as when the majors are all in #s and the minors all in ?s; because when six majors have been generated in #s, they furnish the new notes needed by the six relative minors; and when six minors have been generated in ?s, they furnish the new notes for the six relative majors. This plate begins with the major in C and the minor in A. The notes of these two are all identical except the D, which is the sexual note, in which each is not the other, the D of the minor being a comma lower than the D of the major. Going round by the keys in #s, we come first to E minor and G major. G major has been mathematically generated, and the relative minor E gets its F# from it; but the D of C major must also be [Scientific Basis and Build of Music, page 112]
given to this scale, as the D of A minor would be a comma too low; it would make a 9-comma interval between D and E, the seventh and eighth, where the minor mode has an 8-comma one. So its two new notes are thus found in the relative and sub-relative majors. This is the way of their mutual providing in the region of the #s; the # seventh of the major is given to be the # second of the minor, and the comma-higher second of the sub-relative becomes the seventh of the minor; and then we have a true written representation of what Nature has done. [Scientific Basis and Build of Music, page 113]
Starting again at C major and A minor and going round by the keys in ?s, we come first to D minor and F major. The major gets its ? fourth from the ? sixth of the relative minor; and as the interval between D-E, the major sixth and seventh, must be a 9-comma interval, and its own D-E is only an 8-comma one, it must take the D of A minor, which is a comma lower, and this will correctly show the 9-comma interval between D and E. This is the way of their mutual providing in the region of ?s; the ? sixth of the minor is given to be the ? fourth of the relative major; and the comma-lower fourth of the sub-relative minor becomes the correct sixth of the major. The arrows indicate the source from which, and the place to which; the new notes come and go. [Scientific Basis and Build of Music, page 113]
The Octave being divided into 53 commas, the intervals are measured, as usual, by these, the large second having 9-commas, the medium second having 8, and the small second 5. These measures are then made each the radius by which to draw hemispheres showing the various and comparative areas of the seconds. The comparative areas of the thirds are shown by the hemispheres of the seconds which compose them facing each other in pairs. The comma-measures of the various thirds thus determined are then made the radii by which to draw the two hemispheres of the fifths. The areas of the three fifths are identical, as also the attitudes of their unequal hemispheres. The attitude of the six thirds, on the other hand, in their two kinds, being reversed in the upper and under halves of the scale, their attitude gives them the appearance of being attracted towards the center of the tonic; while the attitude of the three fifths is all upward in the major, and all downward in the minor; their attraction being towards the common center of the twelve scales which Nature has placed between the second of the major and the fourth of the minor, as seen in the two D's of the dual genetic scale, - the two modes being thus seen, as it were, revolving [Scientific Basis and Build of Music, page 113]
One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]
In the festoons of ellipses the signatures are given in the usual conventional way, the major F having one flat and minor E having one sharp. The major and minor keys start from these respective points, and each successive semitone is made a new keynote of a major and a minor respectively; and each ellipse in the festoons having the key shown in its two forms; for example, in the major F, one flat, or E#, eleven sharps; in the minor E, one sharp, or F?, eleven flats. Thus is seen all the various ways that notes may be named. The four minor thirds which divide the octave may be followed from an ellipse by the curved lines on which the ellipses are hung; and these four always constitute a chromatic chord. [Scientific Basis and Build of Music, page 115]
The middle portion with the zigzag and perpendicular lines are the chromatic chords, as it were arpeggio'd. They are shown 5-fold, and have their major form from the right side, and their minor form from the left. In the column on the right they are seen in resolution, in their primary and fullest manner, with the 12 minors. The reason why there are 13 scales, though called the 12, is that F# is one scale and G? another on the major side; and D# and E? separated the same way on the minor side. Twelve, however, is the natural number for the mathematical scales as well as the tempered ones. But as the mathematical scales roll on in cycles, F# is mathematically the first of a new cycle, and all the notes of the scale of F# are a comma and the apotome minor higher than G?. And so also it is on the minor side, D# is a comma and the apotome higher than E?. These two thirteenth keys are therefore simply a repetition of the two first; a fourteenth would be a repetition of the second; and so on all through till a second cycle of twelve would be completed; and the thirteenth to it would be just the first of a third cycle a comma and the apotome minor higher than the second, and so on ad infinitum. In the tempered scales F# and G? on the major side are made one; and D# and E? on the minor side the same; and the circle of the twelve is closed. This is the explanation of the thirteen in any of the plates being called twelve. The perpendicular lines join identical notes with diverse names. The zigzag lines thread the rising Fifths which constitute the chromatic chords under diverse names, and these chords are then seen in stave-notation, or the major and minor sides opposites. The system of the Secondary and Tertiary manner of resolution might be shown in the same way, thus exhibiting 72 resolutions into Tonic chords. But the Chromatic chord can also be used to resolve to the Subdominant and Dominant chords of each of these 24 keys, which will exhibit 48 more chromatic resolutions; and resolving into the 48 chords in the primary, secondary, and tertiary manners, will make 144 resolutions, which with 72 above make 216 resolutions. These have been worked out by our author in the Common Notation, in a variety of positions and inversions, and may be published, perhaps, in a second edition of this work, or in a practical work by themselves. [Scientific Basis and Build of Music, page 115]
These two plates show the chromatic chord resolving into the twelve major and twelve minor tonic chords of the twenty-four scales. There seems to be twenty-five, but that arises from making G? and F# in the major two scales, whereas they are really only one; and the same in the minor series, E? and D# are really one scale. C in the major and A in the minor, which occur in the middle of the series, when both sharps and flats are employed in the signatures, are placed below and outside of the circular stave to give them prominence as the types of the scale; and the first chromatic chord is seen with them in its major and minor form, and its typical manner of resolving - the major form rising to the root, and falling to the top and middle; the minor form falling to the top, and rising to the root and middle. The signatures of the keys are given under the stave. [Scientific Basis and Build of Music, page 116]
The scales in this plate advance by semitones, not in their normal way by fifths; but their normal progress by fifths is shown by the spiral-ellipse line winding round under the stave and touching the ellipses containing the scales by semitonic advance; the scales being read to the right for the majors inside, and to the right for the minors outside. In each of the modes the scales are written in ?s and #s, as is usual in signatures; and since the scales [Scientific Basis and Build of Music, page 116]
advance by semitones, the keys with ?s and #s alternate in both modes. The open between G# and A? in the major, and between D# and E? in the minor, is closed in each mode, and the scale made one. The dotted lines across the plate lead from major to relative minor; and the solid spiral line starting from C, and winding left and right, touches the consecutive keys as they advance normally, because genetically, by fifths. The relative major and minor are in one ellipse at C and A; and in the ellipse right opposite this the relative to F# is D#, and that of G? and E?, all in the same ellipse, and by one set of notes, but read, of course, both ways. [Scientific Basis and Build of Music, page 117]
This plate sets forth the essential duality of the musical system of vibrations. It is a remarkable fact that the numbers of the vibrations of the major mode are the numbers for the string proportions of the minor mode; and vice versa, the string proportions in the major are the numbers of the vibrations in the minor. We have, however, to see that we use the proper notes and numbers; we must know the secret of Nature. This secret rests in the duality of the notes, and begins from the two D's. The center of gravity of the musical system of vibrations is found in the comma space between the |two D's as they are found in the Genesis of the two modes. In these |two D's the vibration number and string proportions are nearly identical. Starting from this point as the center of gravity in the [Scientific Basis and Build of Music, page 118]
dual system, as the strings are shortened the vibrations of course are more, and as the strings are lengthened the vibrations are fewer. This is household lore now; but the new insight and the deeply interesting order of Nature is that the major and the minor contain each other and respond to each other in this striking way; and while manifesting such diversity of character are so essentially one. [Scientific Basis and Build of Music, page 119]
Fig. 1. - This figure shows the major and minor measured in commas and placed directly as they stand related, major and relative minor, the minor being set a minor third lower than the major. The interval between C and E in the minor is an 8-and-9-comma interval; between C and E in the major it is a 9-and-8-comma one. This difference arises from the minor D being a comma lower than the major D. In all the other intervals minor and major are the same. [Scientific Basis and Build of Music, page 120]
Fig. 2. - In this figure the two modes are placed in their inverse relation, in order to show the notes standing opposite each other in their duality. Here the two D's come also opposite each other, inasmuch as in the two modes the C-D-E interval is inverted, becoming C D E in the one and E D C in the other. And so the 9-comma second between C and D in the major comes opposite the 9-comma second between D and E in the minor, and the two 8-comma seconds, of course, come opposite each other also. [Scientific Basis and Build of Music, page 120]
In Fig. 1 is shown the way in which duality arranges the new sharp in the majors to the middle of the dominant, and the new flat to the middle of the subdominant in the minors, all through the six scales done in flats and sharps. The flat goes to the root of the subdominant and the sharp to the top of the dominant in the other six, as in Fig. 2. This is the invariable way that the new sharps and flats are responsively added all through the system. [Scientific Basis and Build of Music, page 120]
Hughes
The inequality of the equinoctial points is a well-known fact. It will be seen how apparent this is in the developments of harmonies. From the moment that trinities depart from unity, the balance is unequal, and the repeated endeavours after closer union cause a perpetual restlessness. May not this want of equilibrium be the life or motive power of the entire universe, with its continuous struggle after concord, even to oneness? "Closer and closer union is the soul of perfect harmony." In tracing harmonies of tones and colours, the double tones of keyed instruments will be seen to correspond with the intermediate tints and shades of colours. The twelve notes, scales, and chords in the major and minor series, the meetings by fifths, &c., all agree so exactly in their mode of development, that if a piece of music is written correctly in colours with the intermediate tints and shades, the experienced musician can, as a rule, detect errors more quickly and surely with the eye than the ear, and the correct eye, even of a non-musical person, may detect technical errors. Although the arithmetical relation has been most useful in gaining the laws, it is not here entered upon; but numbers equally meet all the intricacies both of tones and colours. The bass notes have been omitted, in order to simplify the scheme. [Harmonies of Tones and Colours, The Arabian System of Music, page 21]
THE term "key" in the minor developments must be taken in the sense in which it is understood by musicians, although it will be seen that it is only the seven of the harmony that are the relative minor keys of the majors, the scales with their chords sounding other keys. The grandeur, combined with simplicity, of the laws which develope musical harmonies are strikingly exhibited in the minor keys. Although at first they appear most paradoxical, and, comparing them with the majors, we may almost say contradictory in their laws of development, when they are in some degree understood, the intricacies disappear, and the twelve keys follow each other (with the thirteenth octave), all exactly agreeing in their mode of development. I shall endeavour to trace them as much as possible in the same manner as the majors, the lowest developments of the minor keys being notes with scales and chords, the notes always sounding their major harmonies in tones. Here an apparently paradoxical question arises. If the major keys are gained by the notes sounding the major tones, how are the minor keys obtained? Strictly speaking, there are no minor key-notes: the development of a minor harmony is but a mode of succession within the octave, caused by each minor key-note employing the sharps or flats of the fourth major key-note higher; and with this essential difference, it will be seen in how many points the developments of major and minor harmonics agree. I have carefully followed the same laws, and if any capable mind examines the results, I am prepared for severe criticism. I can only express that it was impossible to gain any other results than the seven of the harmony, the ascending and the descending scale and the chords combining three different keys. [Harmonies of Tones and Colours, Diagram VIII - On the Development of the Twelve Minor Harmonies, page 32]
My first plan was to take away entirely the present development of the Minor Keys; but, on consideration, it seems best to leave them exactly as they are, and to add fresh musical developments of the Minors, explaining them, and leaving it needless, for those who do not wish to look deeper into the subject, to examine the former development. Should they do so, however, they will see that not a single note is altered, the only difference being the Scales developing by fifths instead of by sevenths. [Harmonies of Tones and Colours, Supplementary Remarks, page 54]
I am quite aware that musicians will set aside the Minors as here written; but I trust some minds may be led to examine the beautiful Scriptural types, too deep for our minds ever to find a beginning (the Scriptures have no beginning), and too high for our minds ever to complete ascending. [Harmonies of Tones and Colours, Supplementary Remarks, page 54]
Minor Interval
The Minor Interval is a Major Interval where the upper tone is not found in the Major Scale of the lower and the interval is slightly less distance than a Major Interval.
Just as we have the Major 2nd, 3rd, 6th, 7th and 9th so we also have the Minor 2nd, 3rd, 6th, 7th and 9th.
The Major interval above and right is six steps between the C and A. The Minor Interval to the lower right is marked slightly less or smaller than six steps with the flat sign indicating the A is flattened or slightly lowered in pitch from its natural pitch when found in the Major Scale of C.
Minor Mode
The minor mode or scale form is actually the Aeolian mode of medieval times; the Aeolian mode and the Ionian mode (our present major scale) are the only medieval modes which have been in general use since the Renaissance. The minor mode creates a different impression from the major, because of the difference in the arrangement of the whole and half steps. There are three forms of the minor scale, and each has its own function. These are the natural or pure minor, the harmonic minor, and the melodic minor. [Brye, Joseph; Basic Principles of Music]
Minor Scale
Natural minor has half steps between two and three and between five and six. Harmonic minor has half steps between two and three and between seven and eight, ascending; in descending it usually is natural.
See Also
condensing
falling
female
feminine
Interval
minor chord
minor mode
mode
Mother
relative minor
Scale
