Ramsay
"Finally, when we return to 2?, or 360 degrees around Nature's Grand Fugue (see Ramsey's book Plate I) we end with the "three times three chord", in which the whole 25 notes are struck together, and make that wondrous and restful close of the strange Fugue. No one can hear the thrice-threefold chord of this close an ever forget it: it is "the lost chord" found; and leads the saintly heart away to the Three in One who is the Lord of Hosts; Make of Heaven and Earth, and all the hosts of them." [Dougald Carmichael Ramsay, Scientific Basis and Build of Music, pages 96-104] See also Scientific Basis and Build of Music, pages 17]
It runs in all the polarities of Nature. Music, as belonging to Nature - as one of the things which the Great Numberer hath created - is under this Law of Duality as well as that of mathematical ratios and other laws. The Law of Duality in music gives the major and minor systems. As the major is derived from certain primes in ratios ascending, and the minor from the same primes in the same ratios descending, they are inversely related; and these diatonic scales have in the responding parts exactly the same quantities. But as multiplying by 3 three times gives the framework of the major system in the ascending Genesis, and dividing by 3 three times gives the framework of the minor system in the descending Genesis. They are in this view also directly related. The Law of Duality in music emerges into view from the Genesis [Scientific Basis and Build of Music, page 42]
Having found the framework of the major scale by multiplying F1 three times by 3, find the framework of the minor by dividing three times by 3. But what shall we divide? Well, F1 is the unbegotten of the 25 notes of the great genetic scale; B45 is the last-born of the same scale. We multiply upward from F1 for the major; divide downward from B45 for the minor. Again, B45 is the middle of the top chord of the major system, a minor third below D, the top of that chord, and the top of the whole major chord-scale, so B is the relative minor to it. Now since the minor is to be seen as the INVERSE of the major, the whole process must be inverse. Divide instead of multiply! Divide from the top chord instead of multiply from the bottom chord. Divide from the top of the minor dominant instead of multiply from the root of the major subdominant. This will give the framework of the minor system, B45/3 = E15/3 = A5/3 = D1 2/3. But as 1 2/3 is not easily compared with D27 of the major, take a higher octave of B and divide from it. Two times B45 is B90, and two times B90 is B180, and two times B180 is B360, the number of the degrees of a circle, and two times B360 is B720; all these are simply octaves of B, and do not in the least alter the character of that note; now B720/3 is = E240/3 = A80/3 = D26 2/3. And now comparing D27 found from F1, and D26 2/3 found from B720, we see that while E240 is the same both ways, and also A80, yet D26 2/3 is a comma lower than D27. This is the note which is the center of the dual system, and it is itself a dual note befittingly. [Scientific Basis and Build of Music, page 81]
Three times three are nine; this would give nine notes; but as the top of the first chord serves for the root of the second one, and the top of the second for the root of the third, in this way these three chords of three notes each are formed from seven different notes. [Scientific Basis and Build of Music, page 96]
together on radial lines from the center they appear grouped in various chords and combinations, dropping out and coming in in such succession as to constitute what Ramsay, whose genius was given to set this thus before us, calls "Nature's Grand Fugue." Beginning at F in the center at the top, and moving either to the right or to the left, after a run of 7 notes we have 4 consecutive Octaves, and then comes the Minor fifth, A-E, followed by the Major fifth, G-D; and this by another Major fifth, F-C; the combinations keep changing till at the quarter of the circle we come to F, A, C, E, G, a combination of the subdominant and tonic Major; and after another varied series of combinations we have at the half of the circle the elements of 2 minor chords, D, F, A and A, C, E, and one Major chord, C, E, G; at the third quarter we have a repetition of the first quarter group; and the various chords and combinations dropping out and coming in, fugue-like; finally we return to where we began, and end with the three-times-three chord, in which the whole 25 notes are struck together, and make that wondrous and restful close of this strange Fugue. No one can hear the thrice-threefold chord of this close and ever forget it; it is "the lost chord" found; and leads the saintly heart away to the Three in One who is the Lord of Hosts; Maker of Heaven and Earth, and all the host of them. [Scientific Basis and Build of Music, page 103]
Here on the keyboard we see, nearest to the front, the great 3-times-3 chord of the full genesis of the scale from F1 to F64. When this chord is struck by the notched lath represented in front of the keyboard, the whole harmony of the key is heard at once. Behind this great chord are placed, to the left the subdominant, tonic, and dominant chords of the minor. D F A, A E C, E G B; and to the right the subdominant, tonic, and dominant chords of the major, F A C, C E G, G B D. When the notched lath is shifted from F to D, the minor third below F, and the 3-times-3 minor is struck down in the same way as the major, the whole harmony is heard; and the complete contrast of effect between major and minor harmony can be fully pronounced to the ear by this means. Behind these six diatonic chords, major and minor, on the part of the keyboard nearest to the black keys, are the three chromatic chords in their four-foldness, in both major and minor form. The center one shows the diatonic germ of the chromatic chord, with its supplement of G# on the one hand completing its minor form, and its supplement of A? on the other hand completing its major form. A great deal of teaching may be illustrated by this plate.
When Leonhard Euler, the distinguished mathematician of the eighteenth century, wrote his essay on a New Theory of Music, Fuss remarks - "It has no great success, as it contained too much geometry for musicians, and too much music for geometers." There was a reason which Fuss was not seemingly able to observe, namely, that while it had hold of some very precious musical truth it also put forth some error, and error is always a hindrance to true progress. Euler did good service, however. In his letters to a German Princess on his theory of music he showed the true use of the mathematical primes 2, 3, and 5, but debarred the use of 7, saying, "Were we to introduce the number 7, the tones of an octave would be increased." It was wise in the great mathematician to hold his hand from adding other notes. It is always dangerous to offer strange fire on the altar. He very clearly set forth that while 2 has an unlimited use in producing Octaves, 3 must be limited to its use 3 times in producing Fifths. This was right, for in producing a fourth Fifth it is not a Fifth for the scale. But Euler erred in attempting to generate the semitonic scale of 12 notes by the use of the power of 5 a second time on the original materials. It produces F# right enough; for D27 by 5 gives 135, which is the number for F#. D27 is the note by which F# is produced, because D is right for this process in its unaltered condition. But when Euler proceeds further to use the prime 5 on the middles, A, E, and B, and F#, in their original and unaltered state, he quite errs, and produces all the sharpened notes too low. C# for the key of D is not got by applying 5 to A40, as it is in its birthplace; A40 has already been altered for the key of G by a comma, and is A40 1/2 before it is used for producing its third; it is A40 1/2 that, multiplied by 5, gives C#202 1/2, not C200, as Euler makes C#. Things are in the same condition with E before G# is wanted for the key of A. G# is found by 5 applied to E; not E in its original and unaltered state, E30; but as already raised a comma for the key of D, E30 3/8; so G# is not 300, as Euler has it, but 303 3/4. Euler next, by the same erroneous methods, proceeds to generate D# from B45, its birthplace number; but before D# is wanted for the key of E, B has been raised a comma, and is no longer B45, but B45 9/16, and this multiplied by 5 gives D#227 13/16, not D225, as Euler gives it. The last semitone which he generates to complete his 12 semitones is B?; that is A#, properly speaking, for this series, and he generates it from F#135; but this already altered note, before A# is wanted for the key of B, has been again raised a comma [Scientific Basis and Build of Music, page 107]
Under the symbol of a music plant this plate gives us to realize the growth-like continuity of chords and scales. The roots of the three chords of a key are represented in F, C, and G of the key of C. The plant might be represented as a creeping stem, like the creepers of the strawberry, with its progressive roots struck into the earth; but it is better to show an upward stem with aerial roots, for such are the roots of the musical plant. The main stem of the plant has the three chords, F a C e G b D; that is, F a c, C e g, G b d, the subdominant, tonic, and dominant. The terminal chord, D f# a, is to show that the keys as well as the chords GROW out of each other. Include the side branches which terminate with the octave notes of the chords, read thus - F a c f, G e g e, G b d g, because a chord is felt to be most complete in its unity when thus shut in by the octave note of its root. This is the reason why the great three-times-three chord does not stop at D, the top of the dominant chord, but goes on to the sixth octave of the fundamental root, shutting all in by the great peacemaker, F, in order to preserve the unity of the effect which this chord of chords produces. Before D. C. Ramsay showed that the scale of Harmonics extended to six octaves, it was by teachers of the science of music only extended to four. [Scientific Basis and Build of Music, page 110]
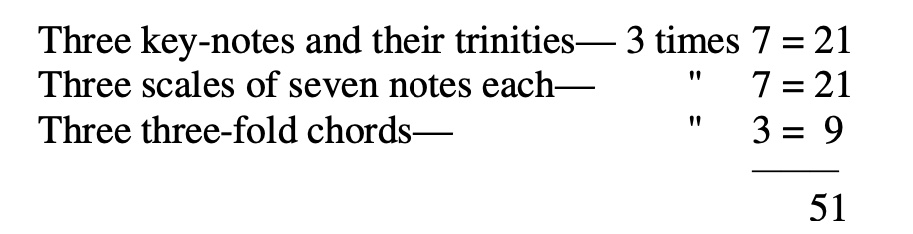
We pass on to the developing of the minor keys. [Harmonies of Tones and Colours, The Twelve Scales Meeting by Fifths, page 31a]
Hear the "three times three chord"
https://s3.amazonaws.com/actual-octaves-and-sono-thermity/Ramsey+25+sounds+in+one+TONE.mp3
See Also
clustered thirds
common chord
Dougald Carmichael Ramsay
major
major system
minor
minor system
Ramsay - Nature's Grand Fugue - The System of Musical Vibrations
Scientific Basis and Build of Music
Scientific Basis and Build of Music - Index
three chords of three notes
three-times-three chord
triplet
