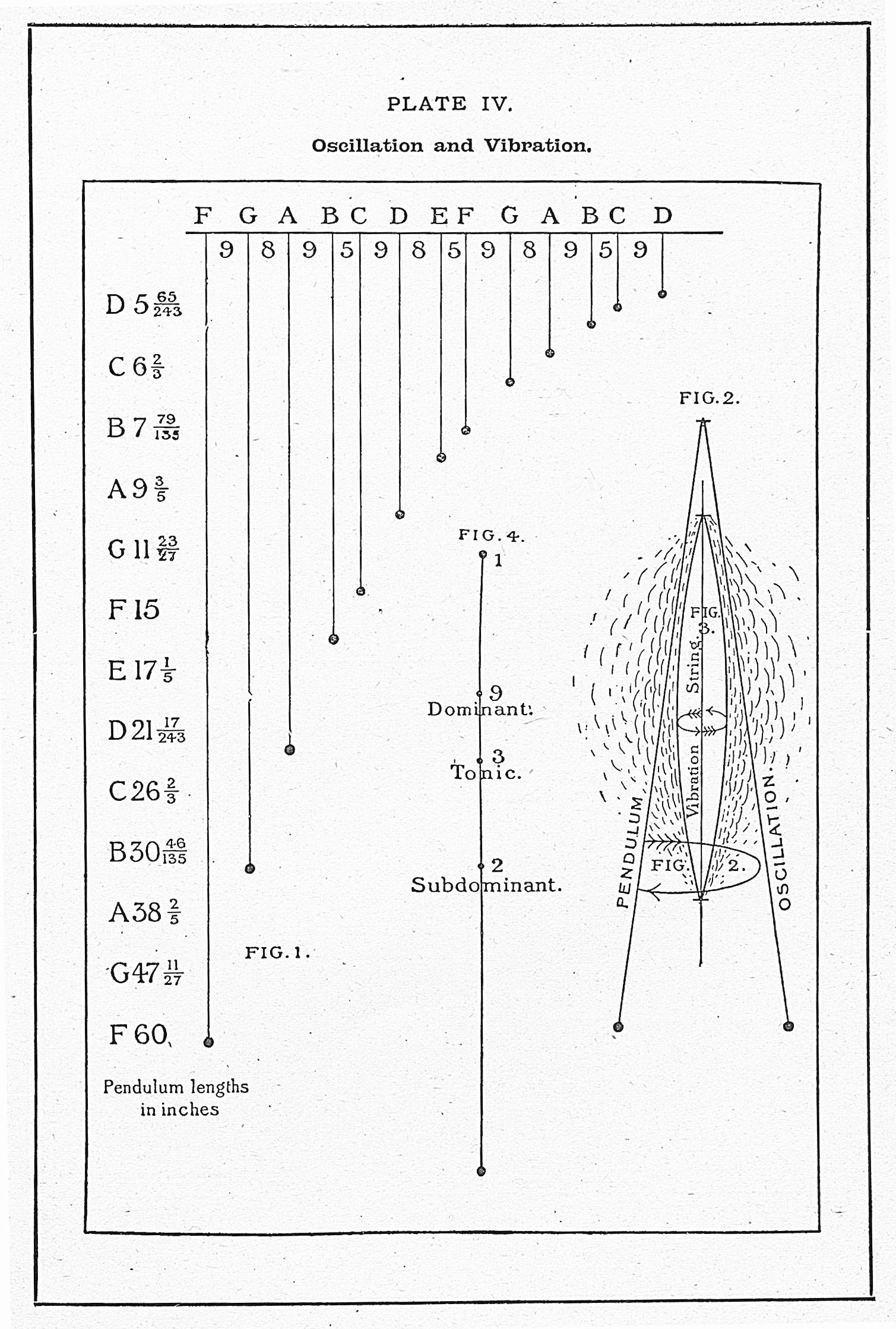
Fig. 1 - The pendulums in this illustration are suspended from points determined by the division of the Octave into Commas; the comma-measured chords of the Major key being S, 9, 8, 9, 5; T, 9, 8, 5, 9; D, 8, 9, 5, 9. The pendulums suspended from these points are tuned, as to length, to swing the mathematical ratios of the Diatonic scale. The longest pendulum is F, the chords being properly arranged with the subdominant, tonic, and dominant, the lowest, center, and upper chords respectively. Although in "Nature's Grand Fugue" there are 25 pendulums engaged, as will be seen by reference to it, yet for the area of a single key 13 pendulums, as here set forth, are all that are required. It will not fail to be observed that thus arranged, according to the law of the genesis of the scale, they form a beautiful curve, probably the curve of a falling projectile. It is an exceedingly interesting sight to watch the unfailing coincidences of the pendulums perfectly tuned, when started in pairs such as F4, A5, and C6; or started all together and seen in their manifold manner of working. The eye is then treated to a sight, in this solemn silent harp, of the order in which the vibrations of sounding instruments play their sweet coincidences on the drum of the delighted ear; and these two "art senses," the eye and the ear, keep good company. Fig. 2 is an illustration of the correct definition of a Pendulum Oscillation, as defined in this work. In watching the swinging pendulums, it will be observed that the coincidences [Scientific Basis and Build of Music, page 104]
are always when they have returned to the side from which they were started. The Pendulographer, also, when writing the beautiful pictures which the musical ratios make when a pen is placed under the control of the pendulums, always finds his figure to begin again when the pendulums have finished their period, and have come for a fresh start to the side from which the period began. This confirms our author's definition of an oscillation of a pendulum. Fig. 3 is an illustration of the correct definition of a Musical Vibration, as also given in this work. Although the definition of an oscillation is not identical with that of a vibration, yet on account of their movement in the same ratios the one can be employed in illustration of the other as we have here done. Fig. 4 is a uniform rod suspended from the end as a pendulum; it will oscillate, of course, at a certain speed according to its length. In such a pendulum there are three centers related in an interesting way to the subject of Music in its three chords - subdominant, tonic, and dominant, which roots are F, C, and G. The center of gravity in the middle of the rod at 2, suspended at which the rod has no motion, corresponds to F, the root of the subdominant, in which there is the maximum of musical gravity. The center of oscillation at 3, which is one-third of the length of the rod from the end, is like the root of the tonic whose number is 3 in the genesis of the scale from F1. In this point of suspension the oscillations are the same as when suspended from the end at 1. The point at 9 is at a ninth from the center of oscillation. Our author discovered that, if suspended at this point, the pendulum had its highest rate of speed. Approaching the end, or approaching the center of oscillation from this point, the rate of speed decreases. Exactly at one-ninth from the center of oscillation, or two-ninths from the end, is this center of velocity, as Ramsay designated it; and it corresponds in some sort also to the root of the dominant G, which is 9 in the genesis of the scale from F1; its rate of vibration is nine times that of F1. The dominant chord is the one in which is the maximum of levity and motion in music. [Scientific Basis and Build of Music, page 105]
See Also
8.20 - Law of Sympathetic Oscillation
Center of Oscillation
co-oscillation
co-vibration
Differential Oscillation
double vibration
Figure 8.11 - Four Fundamental Phases of a Wave
Figure 8.9 - Four Fundamental Motions of a Pendulum
Law of Oscillating Atomic Substances
Law of Variation of Atomic Oscillation by Sono-thermism
Law of Variation of Pitch of Atomic Oscillation by Pressure
laws of oscillatory and vibratory motions
MOLECULAR OSCILLATING FREQUENCY
molecular oscillation
oscillate
oscillating proximately
oscillating range of motion
Oscillation
oscillatory motion
Pendulum Oscillation
Proximate Oscillation
Ramsay - PLATE IV - Oscillation and Vibration
Ramsay - PLATE V - Proximate and Differential Oscillations
Ramsay - The Marshalling of the Host of the Lower Heavens21
Ramsay - The New Way of Reckoning a Pendulum Oscillation
Ramsay - The New Way of Reckoning a Vibration
single vibration
Sympathetic Oscillation
Table 13.02 - Vibratory and Oscillatory Triple Force Functions
TREXNONAR MEASUREMENT OF MOLECULAR OSCILLATING FREQUENCIES
vibration
