| Reciprocal | Reciprocal | |
Sympsionics Symbol | ||
See Covariance
noun: something (a term or expression or concept) that has a reciprocal relation to something else
noun: (mathematics) one of a pair of numbers whose product is 1: the reciprocal of 2/3 is 3/2; the multiplicative inverse of 7 is 1/7
adjective: concerning each of two or more persons or things; especially given or done in return ("Reciprocal aid")
adjective: of or relating to the multiplicative inverse of a quantity or function ("The reciprocal ratio of a:b is b:a")
adjective: of or relating to or suggestive of complementation
[Multiplicative inverse means the same thing as reciprocal.]
Schauberger
Space and volume are inversely disposed opposites, which consume or animate one another depending on whether one is made to burn by the other or
[4] See description of air-turbine in Austrian Patent No. 145141, p. 115 of this book. —Ed.
6
is itself ennobled intrinsically through this reciprocal intensification and polarization. Today's technology mistakenly chose the former of the two processes and it is therefore no wonder that cancer is on the rampage here, there and everywhere.
Goethe said, "The driving wheels of Nature are polarity and intensification and whoever understands enough to untie also knows enough to bind." What is born in light, disintegrates in the coolness of the ground. It rises up and returns again as a ray of energy in order to quicken that which stands ready to become new life at the boundary between space and volume.
Every leaf is an animalistic magnet in monoplanar form, which attracts and radiates, depending on whether the Sun shines on it or cold caresses it. This great law of reciprocity also operates in water, which constantly restructures itself by altering its space and volume. The space is shaped by light and heat. The volume is a product of darkness and coolness. If we understand how to apportion the opposing relation between space and volume and how to organise its intrinsic structure, then the substance - water - will become 'The Space' and the formless volume its realisation, which is transformed instantaneously with heat-pressure, thereby creating the motion that fills the over-lying inter-space.
If nature-alienated humanity, however, reverses this purposeful process and combusts precisely those substances that occasion life, then they should no longer be surprised when the Sun burns up that which serves it as an intermediate space, and which serves humankind for the maintenance of life.
Life unfolds itself in three spheres:
1. in the Carbone[5] - sphere
2. in the Atmosphere
3. in the Stratosphere
The connection between these spheres is created by water. Conversely, the various states of aggregation of water form the bridges for the formation and reconstitution of the basic elements carried by water, which succeed in reaching the Earth's interior from the stratosphere and vice versa. The purely mechanical circulation of the physical form - water - operates in the opposite direction to the circulation of energy. The rising of the C-substances with their carrier - water - is countered by the sinking of the oxygen. Where these
[5] Carbone: In contrast to the normal use and definition of 'carbon', Viktor Schauberger grouped all the known elements and their compounds, with the exception of oxygen and hydrogen, under the general classification of 'Mother Substances', which he described with the word 'Kohle-stoffe', normally spelt 'Kohlenstoffe' and meaning carbon. Apart from the above definition the hyphen also signifies a higher aspect of carbon, both physically and energetically or immaterially. The additional V in the English word is therefore intended to redefine and enlarge the scope of the usual term 'carbon' in accordance with Viktor's concepts. On occasion carbone will be represented by the term C' [to] differentiate it from the normal term for carbon — C - Ed.
7
mutually contra-directional currents intersect, energy is freed. These energetic interactions can never reach a state of rest due to the constant variation in the length of night and day. Inevitably therefore, there is a continual shift in the individual microclimatic conditions, which further result in variations in the quantity and quality of the basic elements. [The Energy Evolution - Harnessing Free Energy from Nature, Conclusions]
Ramsay
Well, how are we to get the true minor scale? There is a remarkable fact, and a beautiful one, which suggests the method. Such is the economy of Nature, that from one system of proportion employed in two different ways, in the one case as periods of vibrations and in the other as quantities of strings, everything in Music's foundation is produced. It is a remarkable fact that the numbers for the lengths of the strings producing the major scale are the numbers of the vibrations producing the minor scale; and the numbers for the lengths of the strings for the minor scale are the numbers of the vibrations of the notes of the major scale. Here Nature reveals to us an inverse process for the discovery of the minor scale of notes. [Scientific Basis and Build of Music, page 31]
In order to find the notes for the next major key above C, we have to multiply the vibration-number of D, which is the top of the dominant C, by 3 and 5. It is out of the key of C at this point that the new key sprouts and grows, and by the primes and method which produce the key of C itself. So if we would find the relative minor of C, let us take the note which is a minor third below D - that is, B - to produce the minor. The minor sprouts and grows from this point of the key of C; for the relative minor grows out of the major, as out of the man at first the woman is taken. Moreover, B is the last-born of the notes for the major scale; for the middles, that is, the thirds of chords, are always produced by the prime 5; and the tops, that is, the fifths of chords, are produced by the prime 3, and are born before the thirds, though placed after them in the chords. Well, because B is the last-born note of the major, as well as a minor third below the top of the highest chord of the major, it seems that the minor should have this for its point of departure. Again, we have seen that the major and the minor are found in their strings and their vibrations by an inverse process, that one going back upon the other; and, there taking Nature's clue, let us proceed by an inverse process of generating the minor. Making B45 our unit, as F1 was our unit for the major, let us divide by 3 and 5 for a root and middle to B, as we multiplied by 3 and 5 for a top and middle to F. B45 divided by 3 is 15; here then is our E, the root of the chord, just where we had found it coming upward; for, remember, we found E15 by multiplying C3 by 5. This E, then, is the same in major and minor. Now B45 divided by 5 is 9; [Scientific Basis and Build of Music, page 31]
It is in their inverse relations that the major and the minor are equal. Every note, chord, and progression in the one has its reciprocal or corresponding note, chord, and progression in the other. This is the Law of Duality. And this general law of Nature is so deeply rooted in music, that is the numbers which represent the vibrations in the major system be made to represent quantities of string, these quantities will produce the minor system (beginning, of course, with the proper notes and numbers); so that when the quantities are minor the tones are major, and when the quantities are major the tones are minor.1[Scientific Basis and Build of Music, page 44]
All the inverse and reciprocal orders in music, whether of notes or chords, are produced by the law of Duality, and this gives them inevitably their symmetrical form. [Scientific Basis and Build of Music, page 79]
This plate sets forth the essential duality of the musical system of vibrations. It is a remarkable fact that the numbers of the vibrations of the major mode are the numbers for the string proportions of the minor mode; and vice versa, the string proportions in the major are the numbers of the vibrations in the minor. We have, however, to see that we use the proper notes and numbers; we must know the secret of Nature. This secret rests in the duality of the notes, and begins from the two D's. The center of gravity of the musical system of vibrations is found in the comma space between the |two D's as they are found in the Genesis of the two modes. In these |two D's the vibration number and string proportions are nearly identical. Starting from this point as the center of gravity in the [Scientific Basis and Build of Music, page 118]
See Also
Balance
countervail
Covariance
Conjugate Variables
Figure 12.13 - Some Multi-Dimensional as Inverse and Direct Reciprocal Relationships
Figure 13.14 - Equilibrium as Reciprocal Forces
Figure 3.10 - Temperature Accumulates in the North and Cools in the South Reciprocally
Fraction
inverse
mate-pairs
Multiplicative inverse
opposite
Ratio
Law of Ratios
Reciprocating Proportionality
Rhythmic Balanced Interchange
Rotation and Revolution are Reciprocals
Seesaw
sympathetic vibratory interchange
3.13 - Reciprocals and Proportions of Motions and Substance
6.1 - Reciprocal Radiations
7.3 - Law of Love - Reciprocal Interchange of State on Multiple Subdivisions
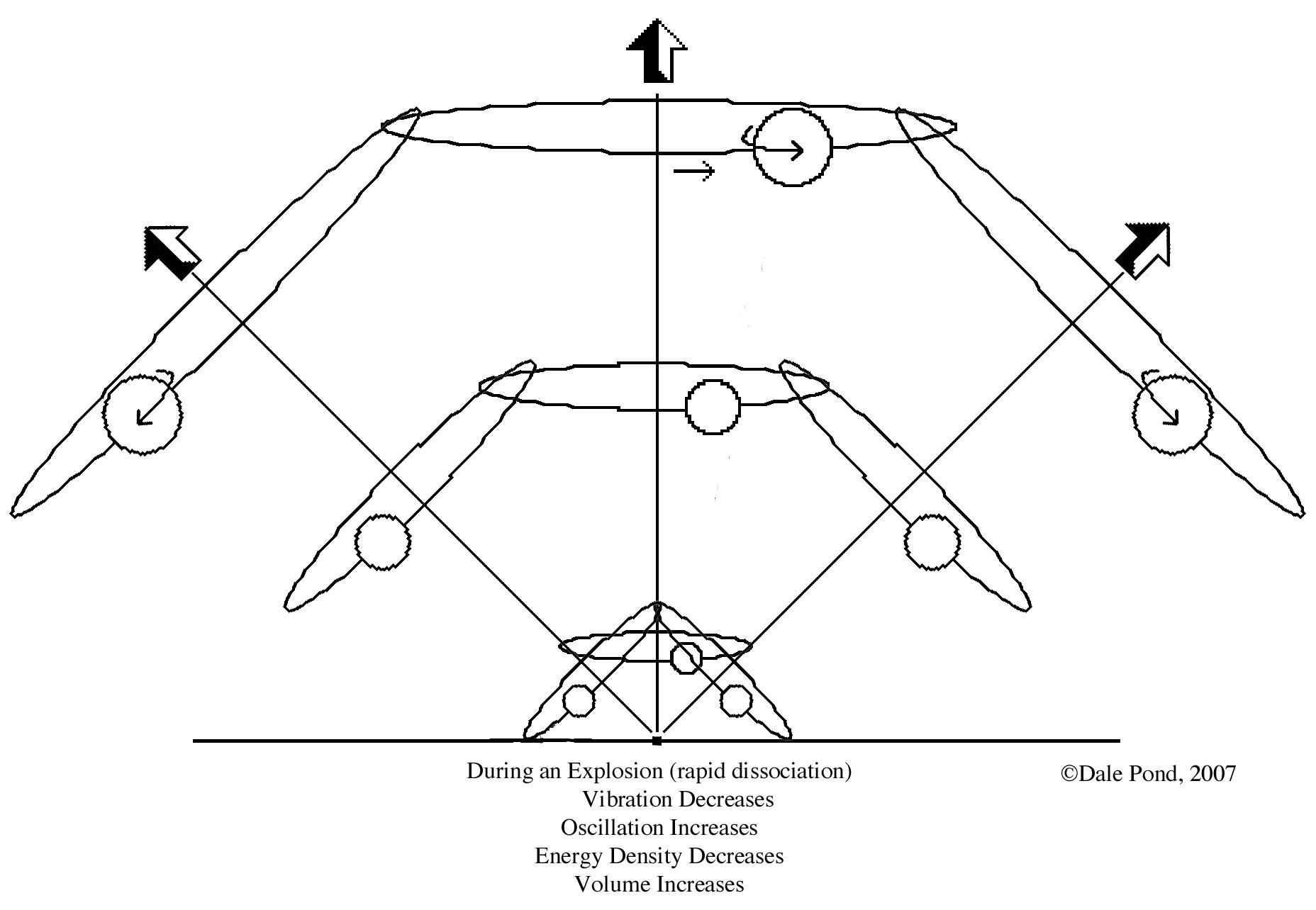
7.6 - Reciprocal Disintegration and Creation
7.7 - Reciprocal States of Matter and Energy
12.00 - Reciprocating Proportionality