Sympathetic Vibratory Physics

Schauberger
These guide-vanes are placed at certain intervals so that mechanical pressure is alternately increased and decreased continuously. This results in the cooling of the whole water-mass, similar to the Linde process[15], only that here [The Energy Evolution - Harnessing Free Energy from Nature, The Liquefaction of Coal by Means of Cold Flows]

Solomons Musical Glossary
The distance between two pitches or notes. Intervals may be measured in a number of ways; e.g., by counting the number of semitones, subtracting frequencies, etc. Counting semitones is used in set theory. However, the most common method is by counting letter names; e.g. C, D, E, F includes 4 letters - thus, C to F is called a fourth and is always a fourth, no matter how the notes may be altered by sharps or flats. This is called the "general size" of the interval. However, each general interval may have several "specific sizes"; e.g. a third could be major, minor, diminished, augmented, etc. The specific size is determined by 1. the general size, and 2. the number of semitones it contains. [Solomons Musical Glossary]

The distance in pitch between two notes, harmonic if they are played together, melodic if they are played in succession.
Perfect : the prime, fourth, fifth, and octave.
Major : the second, third, sixth, and seventh of the major scale.
Minor : a chromatic half step smaller.
Augmented : a chromatic half step larger than perfect and major.
Diminished : a chromatic half step smaller than perfect and minor.

An interval is a combination of two tones. It is also the distance between or the difference between two tones. When these two tones are sounded together the result is an harmonic interval, and when they are sounded one after the other the result is a melodic interval. The quality of an interval is determined by its size and by the relationship of its position to the keynote.

Augmented Interval A musical interval slightly increased in pitch by the addition of a sharp. Diminished Interval A perfect or minor interval reduced by a semitone.

Perfect Interval The Perfect Interval is a Major Interval where the lower tone is found in the Major Scale of the upper tone as well as the upper tone is found in the Major Scale of the lower tone. The Major 6th to the right is Major as D is part of the Major Scale of F but F is not part of the Major Scale of D. Therefore it is not a Perfect Interval. The Perfect Fourth to the lower right is Perfect because F is found in the Major Scale of C and C is found in the Major Scale of F. Perfect Intervals may be a 1st, 4th, 5th and 8th.

There are six types of intervals: semitone, major (indicated by M), minor (m), perfect (P), diminished (dim.), and augmented (Aug.).

A semitone is an interval smaller than a full interval.

A major interval contracted - by lowering the upper note or raising the lower note - by one half step becomes minor, and contracted by another half step becomes diminished.

A perfect interval contracted by a half step becomes diminished, and contracted by another half step (not usually practical), becomes doubly diminished.

A perfect or a major interval expanded by a half step becomes augmented. [Byre, Joseph; Basic Principles of Music]

The distance in pitch between two notes, which is expressed in terms of the number of notes of the diatonic scale which they comprise (e.g. third, fifth, ninth) and a qualifying word (perfect, imperfect, major, minor, augmented, or diminished). The number is determined by the position of the notes on the staff, the qualifying word by the number of tones and semitones in the interval. Thus (no clef) C - G is always a third, while (F clef) C - G is a major third, being a distance of two tones, and (G clef) C - G is a minor third, being a distance of a tone and a half. [Collin's Music Encyclopedia]

Click Here to Calculate Music Intervals in any Octave

Table of Music Intervals

[This table begins with C. Ramsay begins his tables with F.]

Note	Interval	Ratio	Numerator	Denominator	Decimal
C	First	1:1	1	1	1
	Apotome Minor
	Apotome
	Comma
	Pythagorean Comma	81:80	81	80	0.9765625
	Enharmonic	128:125	128	125	0.9765625
	Lesser Diesis	128:125	128	125	0.9765625
	Greater Diesis	648:625	128	125	0.96450617
C#	Lesser Chromatic Semitone	25:24	25	24	0.96
	Leimma	256:243	256	243	0.94921875
	Greater Chromatic Semitone	135:128	135	128	0.94814815
	Minor Semitone	17:16	17	16	0.94117647058824
	Major (Diatonic) Semitone	16:15	16	15	0.9375	Law of Proximity
D?	Minor Second	27:25	27	25	0.925993
	Minor Tone	10:9	10	9	0.9	Law of Proximity
D	Major Second	9:8	9	8	0.8888889
D#	Augmented Second	75:64	75	64	0.853333333
	Minor Third (Pythagoras)	32:27	32	27	0.84375
E?	Minor Third	6:5	6	5	.833333333
E	Major Third	5:4	5	4	0.8
	Major Third (Pythagoras)	81:64	81	64	0.79012345679012
E#	Diminished Fourth	32:25	32	25	0.78125
F?	Augmented Third	125:96	125	96	0.768
F	Perfect Fourth	4:3	4	3	0.75	Law of Affinity
F#	Augmented Fourth	25:18	25	18	0.72
	Tritone	45:32	45	32	0.711111111
	Diminished Fifth	64:45	64	45	0.703125
G?	Diminished Fifth	36:25	36	25	0.69444444
G	Perfect or Major Fifth	3:2	3	2	0.66666667	Law of Affinity
G#	Augmented Fifth	25:16	25	16	0.64
A??
A?	Minor Sixth	8:5	8	5	0.625
A	Major Sixth	5:3	5	3	0.6
A#	Augmented Sixth	125:72	125	72	0.576
	Harmonic Seventh	7:4	7	4	0.57142857142857
	Dominant or Minor Seventh	16:9	16	9	0.5625
B?	Minor or Tonic Seventh	9:5	9	5	0.55556
B	Major Seventh	15:8	15	8	0.53333
B#	Diminished Octave	48:25	48	25	0.52083333
C??
C?	Augmented Seventh	125:64	125	64	0.512
C	Octave	2:1	2	1	0.5	Law of Affinity
	Minor Ninth	32:15	32	15	0.46875
	Major Ninth	9:4	9	4	0.44444444
	Harmonic or Minor Tenth	7:3	7	3	0.42857143
	Minor Tenth	12:5	12	5	0.4166667
	Major Tenth	5:2	5	2	.4
	Perfect Eleventh	8:3	8	3	0.375
	Harmonic Eleventh	11:4	11	4	0.363636
	Augmented Eleventh	45:16	45	16	0.355556
	Perfect Twelfth	3:1	3	1	0.333333
	Augmented Twelfth	25:8	25	8	0.32
	Minor Thirteenth	16:5	16	5	0.3125
	Harmonic Thirteenth	13:4	13	4	0.30769231
	Major Thirteenth	10:3	10	3	0.3
	Harmonic Fourteenth	7:2	7	2	0.28571429
	Dominant Fourteenth	32:9	32	9	0.28125
	Tonic Fourteenth	18:5	18	5	0.27777778
	Major Fourteenth	15:4	15	4	0.26666667
	Double Octave, Fifteenth	4:1	4	1	0.25

[Some notes from Professor Haughton's "Natural Philosophy", page 181.
Some intervals from Scientific Basis and Build of Music.]

Ramsay
"While vibrations are the sound-stuff, the protoplasm of notes, semitones are, as it were, the atoms of which music is composed. We may think and talk of quarter tones and commas, apotomes and skismas, and dots, but these have no place as intervals for the musical ear, nor any part in the compositions which so charm us of the great masters." [Scientific Basis and Build of Music, page 20]

"centrifugal force. A third note produced by the prime 5 is derived from the note produced by the first power of 3, and this note by the first power of 5 having being slightly acted on by the force of gravity, and the first power of 5 having only a little centrifugal force, the result is that this note E in the scale of C, derived from the first power of 3 by the prime 5, is balanced between the two forces. It is the only note in the system which in the octave scale has not a large interval on the one side of it nor on the other, and consequently it is the only note which attracts and is attracted by two notes from proximity. Thus it is that the musical system is composed of three notes having specific gravity and three having specific levity or bouyancy, and one note, E, the center of the tonic chord, balanced between these two forces. As the attractions of notes from proximity take place when the notes with downward tendency meet the note with upward tendency, had the notes been animated by only one of these forces there could have been no system of resolutions of the notes either in melody or harmony; they would all have been by gravity weighing it downwards, or by levity soaring upwards." [Scientific Basis and Build of Music, page 28]

The law of gravitation is the law of Music as well as of Astronomy. The cycles of the distances, that is the intervals, in Music correspond to the cycles of the periods in Astronomy. In Astronomy the distances and quantities of matter are primary, and determine the periods; in Music the periods and quantities are primary, and determine the distances or intervals. In Astronomy the distances are commensurable; in Music the periods are commensurable. In Astronomy the periods are incommensurable; in Music the distances or intervals are incommensurable. In Astronomy, because the simplicity is not in the periods, the conjunctions are very few at one time; in Music, because the simplicity is in the periods, the conjunctions are very many at one time. And herein lies in the one case the harmony and permanence of the solar system, and in the other case the harmony and beauty of the musical system. The periods and distances in Astronomy and Music are inversely related. [Scientific Basis and Build of Music, page 30]

The life-force of the notes from the law of position gives them a versatility which they could never have had from fixed ratios, however numerous. If the interval of the octave be excepted, there are no two notes together in a chord, nor succeeding each other in the octave scale, having the same amount of specific levity or gravity; consequently each note has an expression and [Scientific Basis and Build of Music, page 35]

character of its own. And as Nature has constituted them, these various forces all converge to the Center of the Tonic Chord, and, with the exception of the interval of the octave itself, the notes of the tempered scale being a little nearer each other than the mathematically perfect notes, these converging forces and this tempering mutually assist each other, and give a greater decision to the resolution of chords. [Scientific Basis and Build of Music, page 36]

A grave harmonic is a secondary note which spontaneously arises when two different notes are sounded together. It is a note whose mathematical number is the difference of the two which awaken it; e.g., F2 and C3, the interval of the fifth, awakens a grave harmonic whose number is 1, which is the difference of 2 and 3; and this 1 strengthens F2, for it is its lower octave. But the interval of F2 and F4, or any other octave, does not awaken a grave harmonic, since there is no difference-number between the two. - Editor. [Scientific Basis and Build of Music, page 36]

If the effects of notes and chords had depended entirely on their mathematical ratios, then the effect of the subdominant, tonic, and dominant would have been alike; for these three chords have exactly the same ratios. It is the law of position which gives the tonic chord its importance, and not any special ratios embodied in its structure. The ratio of 2 to 1 has a pure, unmixed, invariable character, always realized in the interval of the octave. The notes produced from 1 by the first, second, and third powers of 3 have different degrees of centrifugal force. The character of the notes produced by the first power of 5 depends on the character of the notes from which they are derived, namely, 1, 3, and 9. The final character of the notes and chords derived by the same ratios is determined by the amount of force which they have acquired from the way in which they have been derived, and from their position in the system; and no matter where these notes may afterwards be [Scientific Basis and Build of Music, page 37]

Here, then, we have an order of modes entirely symmetrical in pairs placed thus; the only mode that can stand alone being the Dorian, built on D, whose duality has been discovered to reside in itself. All this build of symmetry, which was the watchword of Greek art, as it is also one of the watchwords of Nature, presupposes that the tones of the scale, with lesser and larger intervals lying between them, were resting in their ears exactly as they are in ours,¹ and as they are in all humanity, save where it has sunk down into the savage condition, benighted in the evil that is in the world. It is not to be concluded that the Dorian mode is Nature's primitive scale, although it might have a certain pre-eminence [Scientific Basis and Build of Music, page 45]

Nature has not finished when she has given us the Diatonic Scale of notes as first generated. In the diatonic scale, in ascending from C, the root of the tonic, the first step is an interval of 9 commas, supposing that we adopt the common division of the octave into 53 commas, which is the nearest practical measuring rule; the second step has 8 commas; the third has 5; the fourth has 9; the fifth has 8; the sixth has 9; and the seventh and last has 5 commas. So we have three steps of 9 commas, two steps of 8, and two of 5. The order of the steps in the major is 9, 8, 5, 9, 8, 9, 5. In the minor the magnitudes are the same, but the order is 9, 5, 8, 9, 5, 9, 8. So there are three magnitudes.¹ But Nature has an equalizing process in the course of her musical marshallings, in which these greater ones get cut down, and have to change places with the lesser, when her purpose requires them so to do. [Scientific Basis and Build of Music, page 47]

It should not be supposed that this division of the notes into semitones, as we call them, is something invented by man; it is only something observed by him. The cutting of the notes into twelve semitones is Nature's own doing. She guides us to it in passing from one scale to another as she builds them up. When we pass, for example, from the key of C to the key of G, Nature divides one of the intervals into two nearly equal parts. This operation we mark by putting a # to F. We do not put the # to F to make it sharp, but to show [Scientific Basis and Build of Music, page 47]

that Nature has done so.¹ And in every new key into which we modulate Nature performs the same operation, till in the course of the twelve scales she has cut every greater note into two, and made the notes of the scale into twelve instead of seven. These we, as a matter of convenience, call semitones; though they are really as much tones as are the small intervals which Nature gave us in the genesis of the first scale between B-C and E-F. She only repeats the operation for every new key which she had performed at the very first. It is a new key, indeed, but exactly like the first. The 5 and 9 commas interval between E and G becomes a 9 and 5 comma interval; and this Nature does by the rule which rests in the ear, and is uttered in the obedient voice, and not by any mathematical authority from without. She cuts the 9-comma step F to G into two, and leaving 5 commas as the last interval of the new key of G, precisely as she had made 5 commas between B and C as the last interval of the key of C, she adds the other 4 commas to the 5-comma step E to F, which makes this second-last step a 9-comma step, precisely as she had made it in the key of C.² [Scientific Basis and Build of Music, page 48]

not follow that these are their proper names. In the first chromatic chords, in its major form, B, D, F, A?, G is supposed to be the root; and accordingly the interval from G to A? has been called "a minor ninth;" from B to A? "a diminished seventh;" and from A? to B "an extreme sharp second." These names will vanish like mist of the morning when the intervals so named are seen in the system to which they belong. [Scientific Basis and Build of Music, page 52]

The dominant seventh, G, B, D, F, a 4-note chord,¹ only requires that the root G be made sharp, which will make G#-B a minor third agreeably with the structure of the other two intervals, B-D and E-F. The chromatic chord only differs from the dominant seventh in that it is wholly of minor thirds. There are four notes in a chromatic chord, but only three of them move by semitonic progression to a tonic chord. When these three notes thus move to a major chord, one is upward to the root, a second downward to the top, and the third downward also to the middle. The relative minor being a minor third below [Scientific Basis and Build of Music, page 52]

(click to enlarge)

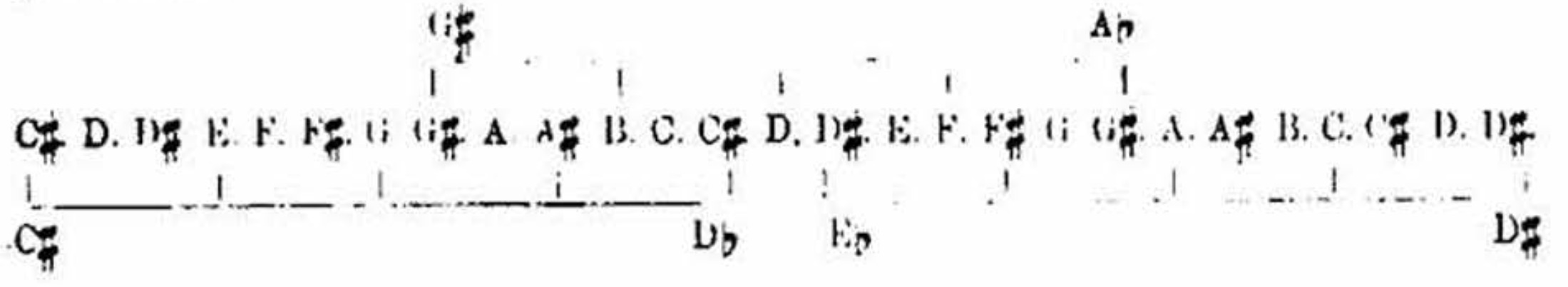
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]

At the extremes of these two operations we find D the top of the major dominant, and D the root of the minor subdominant; and while all the other notes, whether produced by multiplication of the major roots or division of the minor tops, are the same in their ratio-numbers, the two D's, by no speciality of production, are nevertheless specifically diverse by one comma in their vibration-number, and make a corresponding diversity in the intervals of the two modes. These, the Ray and Rah of the Sol Fa expression, originate a very interesting and somewhat mysterious feature in this great twofold genetic scale. [Scientific Basis and Build of Music, page 67]

Chords in a harmony are not at liberty to succeed each other in the way that single notes in a melody may. The notes in a melody may succeed in seconds, or they may succeed in larger intervals, any interval in the octave, even sometimes very effectively there may be a leap or fall of a whole octave. Chords cannot follow each other in this free way; they are under law, and must succeed accordingly. Their law is that they must be linked together either by having something in common in their elements, or have small intervals, semitonic progressions, between them. The former way, by notes in common, is the most usual way in diatonic succession of chords, the latter way, by semitonic progression, is a chief feature and charm in chromatic succession; but both in diatonic and chromatic progression of chords in harmony, notes in common and semitonic progression are usually found together. [Scientific Basis and Build of Music, page 68]

If it be asked why no more primes than 2, 3, and 5 are admitted into musical ratios, one reason is that consonances whose vibrations are in ratios whose terms involve 7, 11, 13, etc., would be less simple and harmonious than those whose terms involve the lesser primes only. Another reason is this - as perfect fifths and other intervals resulting from the number 3 make the schism of a comma with perfect thirds and other intervals resulting from the number 5, so intervals resulting from the numbers 7, 11, 13, etc., would make other schisms with both those kinds of intervals. [Scientific Basis and Build of Music, page 75]

There is no one musical interval which is the perfect measuring rule for the others. But the octave has been divided into 53 parts called commas, and these commas are as near a commensurable rule as we need seek for measuring the musical intervals; always remembering that, strictly speaking, these intervals are incommensurable. The large second has 9 commas; the medium second has 8; and the small second 5; and all other intervals, being of course composed of some of these seconds, can be measured accordingly. Thus the comma, though not itself an interval of our musical system, is the handy and sufficiently perfect inch, let us call it, for practical purposes in music. [Scientific Basis and Build of Music, page 75]

Taking the seven notes of the octave, we have among them 42 intervals in all, without including the octave. When two notes are sounded together, [Scientific Basis and Build of Music, page 76]

the excess of the vibrations of the one note over the other makes one or more sounds which are called "grave harmonics;" e.g., in the interval of the fifth, in the ratio of 2:3, the excess of 3 over 2 is 1, so the grave harmonic is an octave below the lowest of the two notes, that is, the ratio of 1:2. This reinforces the lowest note, 2, and gives it a solid effect. In this way the octave is incorporated into the fifth, and unity with variety is combined with the law of continuity at the very threshold of harmony. In 32 of the 42 intervals the grave harmonics are notes which belong to the natural scale. In the 10 remaining intervals which have not the exact number of vibrations found anywhere in the natural scale, 6 of them are from the number 7, thus - 7, 7, 7, 21, 21, 35; the remaining 4 are from 11, 13, 13, and 19. [Scientific Basis and Build of Music, page 77]

At the first, in the laws of quantities and motions adjusting musical vibrations, there is one chord of the three notes, F, A, C, the root, middle, and top of the five notes which compose the true natural scale; this one chord can be reproduced a fifth higher, C, E, G, in the same mathematical form, taking the top of the first for the root of the second chord. In like manner this second can be reproduced another fifth higher, G, B, D, still in the same mathematical form, and so fit to be a member of the chord-scale of a key. But the law does not admit of another reproduction without interfering with the first chord, so that a fourth fifth produces no new effect; but the whole key is simply a fifth higher, i.e., if the fourth fifth has been properly produced by multiplying the top of the third fifth by 3 and by 5, the generating primes in music. That this carries us into a new scale is seen in that the F is no longer the F? but F#, and the A is no longer A? but A,. But if we suppose the fourth fifth to be simply the old notes with their own vibration numbers, then D, F, A would not be a fifth belonging either to the major or the minor mode, but a fifth a comma less. The letters of it would read like the minor subdominant, D, F, A; but the intervals, as found in the upward development of the major genesis, instead of being, when expressed in commas, 9, 5, 8, 9, which is the minor subdominant, would be 8, 5, 9, 8, which is not a fifth of the musical system; these having always, whether major or minor, two 9's, one [Scientific Basis and Build of Music, page 77]

circumstances. And if we may add D to the subdominant chord of d F A C, so we may also, in other circumstances, add the subdominant chord as harmony to D, thus - D f a c, and no discord occur. There is only the interval of a second between F and G in this dominant 9th, and only an interval of a second between C and D in this subdominant 6th; a second standing alone is a discordant interval, as a poison by itself may kill; but as a poison by the processes of nature in chemistry compounded with something else may be an excellent medicine, so may a second when mixed and compounded with something else in music become an excellent harmony. Music is a great apothecary, skillful in compounds. [Scientific Basis and Build of Music, page 81]

third; and in order to do so, A has been mathematically raised a comma, which makes G A B now a 9-8 comma third. E F G, which in the scale of C was a 5-9 comma third, must now take the place of A B C in the scale of C, which was a 9-5 comma third; and in order to do so, F is mathematically raised 4 commas, and must be marked F#; and now the interval is right for the scale of G. E F# G is a 9-5 comma interval. This mathematical process, in the majors, puts every scale in its original form as to vibration-numbers; but since the same letters are kept for the naming of the notes, they must be marked with commas or sharps, as the case may be. In the Sol Fa notation such marks would not be necessary, as Do is always the key-note, Ray always the second, and Te always the seventh. [Scientific Basis and Build of Music, page 83]

The interval F G A, which in the scale of A was a 9-8-comma interval, must take the place of C D E of the scale of A, which is an 8-9-comma interval; and in order to do this, G has been mathematically lowered a comma. As the middle of the dominant in the major is raised a comma, so the root of the subdominant is lowered a comma. The interval A B C, which in the scale of A was a 9-5-comma interval, is here to take the place of E F G in the scale of A, which is a 5-9-comma interval; and in order to do so, B is lowered 4 commas, and so becomes ?B; and this mathematical process makes the new scale exactly like the old one. This is the way of the minors when calculated as a descending series of scales, which is their natural way. [Scientific Basis and Build of Music, page 84]

are attracted to each other by affinity. But the case is quite different with F and G and C and D. The second fifth above F is G (F a c, C e g), and G becomes the interval above F in the octave scale; and these two notes are neither attracted by affinity nor proximity nor gravitating tendency. F sinks away from G, being heavier, and under it; and G soars away from F, being above it, and lighter. In a similar way the second fifth above C is D (C e g, G b d), and D in the octave scale becomes the interval of the second above C, and C and D, like F and G, are not attracted by either affinity or proximity. C is heavier than D, and being under it would sink away from it; D is lighter, and being above it would soar away from it, and so neither are they attracted by gravitating tendency. [Scientific Basis and Build of Music, page 96]

VIOLIN-FINGERING - Whenever the third finger is normally fourth for its own open string, then the passage from the third finger to the next higher open string is always in the ratio of 8:9; and if the key requires that such passage should be a 9:10 interval, it requires to be done by the little finger on the same string, because the next higher open string is a comma too high, as would be the case with the E string in the key of G. In the key of C on the violin you cannot play on the open A and E strings; you must pitch all the notes in the scale higher if you want to get [Scientific Basis and Build of Music, page 99]

the use of these two open strings in the key of C, on account of the intervals from G to A and from D to E being the ratio of 9:10, the medium second in the scale. G, the third finger on the third string, to A, the open second string, and D, the third finger on the second string, to E, the open first string, being in ratio of 8:9, the large second, you must either use the fourth finger for A and E, or use all the other notes a comma higher. But if thus you use all the notes a little higher, so as to get the use of the A and E strings open, then you cannot get the use of the G and D strings open. On the other hand, in this key of C, if you use the G and D strings open, you cannot use the A and E strings open. One might think the cases parallel, but they are not; because you have a remedy for the first and second open strings, but no remedy for the other two. The remedy for the first and second open strings is to put the fourth finger on the second and third strings for the E and A; but it would be inconvenient, if not impossible, to use the other two strings, G and A, by putting the first finger a comma higher than the open string. [Scientific Basis and Build of Music, page 100]

Whatever interval is sharpened above the tone of the open string, divide the string into the number of parts expressed by the larger number of the ratio of the interval, and operate in that part of the string expressed by the smaller number of it. For example, if we want to get the major third, which is in the ratio of 4:5, divide the string into five parts and operate on four. The lengths are inversely proportional to the vibrations. [Scientific Basis and Build of Music, page 100]

The middle Fig. is the same, the central D's being made a pivot point on which to turn the minor down against the major in an inverse relation, setting the dual notes in file. The multiplying primes are set over the roots. The arrows point out the notes so found. The two D's are here seen right opposite of each other, because the intervals between C D in the major and E D in the minor are equal. [Scientific Basis and Build of Music, page 103]

PLATE VI.

THE AREA OF A SCALE.

This plate is a representation of the area of a scale; the major scale, when viewed with the large hemisphere, lowest; the minor when viewed the reverse way. It is here pictorially shown that major and minor does not mean larger and smaller, for both modes occupy the same area, and have in their structure the same intervals, though standing in a different order. It is this difference in structural arrangement of the intervals which characterizes the one as masculine and the other as feminine, which are much preferable to the major and minor as distinctive names for the two modes. Each scale, in both its modes, has three Fifths - subdominant, tonic, and dominant. The middle fifth is the tonic, and its lowest note the key-note of the scale, or of any composition written in this scale. The 53 commas of the Octave are variously allotted in its seven notes - 3 of them have 9 commas, 2 have 8, and 2 have 5. The area of the scale, however, has much more than the octave; it is two octaves, all save the minor third D-F, and has 93 commas. This is the area alike of masculine and feminine modes. The two modes are here shown as directly related, as we might figuratively say, in their marriage relation. The law of Duality, which always emerges when the two modes are seen in their relationship, is here illustrated, and the dual notes are indicated by oblique lines across the pairs. [Scientific Basis and Build of Music, page 106]

It will be observed that this plate represents intervals by its areas, that is, the distances between the notes; and the notes themselves appear as points. But it must be remembered that these distances or intervals represent the vibrations of these notes in the ratios they bear to each other. So it is the vibration-ratios which constitute the intervals here pictorially represented as areas. The area, as space, is nothing; the note itself is everything. [Scientific Basis and Build of Music, page 107]

PLATE IX.

CLASSIFICATION OF INTERVALS.

There are 42 intervals exclusive of the octave interval with ratio 1:2. There are seven seconds of three magnitudes, so determined in the genesis of notes - two in the ratio of 15:16; two, 9:10; and three, 8:9. There are seven corresponding sevenths - two in the ratio of 8:15; two, 5:9; and three. 9:16. There are seven thirds - one in the ratio of 27:32; three, 5:6; and three, 4:5; and there are seven corresponding sixths - three in the [Scientific Basis and Build of Music, page 109]

ratio of 5:8; three, 3:5; and one, 16:27. There are seven fifths - one in the ratio of 45:64; one, 27:40; and five, 2:3; and seven corresponding fourths - five in the ratio 3:4; one, 40:54; and one 32:45. These are the ratios of the intervals in their simplest expressions as given in the second outer space above the staff in the plate. In the outer space the intervals are given less exactly, but more appreciable, in commas. The ratios of the vibration-numbers of each interval in particular, counting from C24, are given in the inner space above the staff. These vibration-numbers, however, are not given in concert pitch of the notes, but as they arise in the low audible region into which we first come in the genesis from F1, in the usual way of this work. The ratios would be the same at concert pitch; Nature gives the numbers true at whatever pitch in the audible range, or in the low and high silences which lies out of earshot in our present mortal condition. [Scientific Basis and Build of Music, page 110]

It is very interesting to observe how the number seven, which is excluded from the genesis of the system of vibration, comes into view after the genesis is completed, not only in the seven seconds of the melodic scale, but also in the seven of each of the intervals. As there are seven days in the week, though the seventh was only after the genesis of creation was finished, so there are six intervals, but seven of each, as we have seen; and in each 7-fold group three magnitudes determined by the three genetic magnitudes of the seconds. There is much symbolic meaning in all this. Any of the intervals may be used in melody; in harmony also, either in simple or compound chords, they all have the honor of fulfilling a part; and even those, such as seconds and sevenths, which are less honorable in themselves, have great honor in compound chords, such as dominant sevenths and compound tonics, which fulfill exceedingly interesting functions in the society of chords. [Scientific Basis and Build of Music, page 110]

given to this scale, as the D of A minor would be a comma too low; it would make a 9-comma interval between D and E, the seventh and eighth, where the minor mode has an 8-comma one. So its two new notes are thus found in the relative and sub-relative majors. This is the way of their mutual providing in the region of the #s; the # seventh of the major is given to be the # second of the minor, and the comma-higher second of the sub-relative becomes the seventh of the minor; and then we have a true written representation of what Nature has done. [Scientific Basis and Build of Music, page 113]

Starting again at C major and A minor and going round by the keys in ?s, we come first to D minor and F major. The major gets its ? fourth from the ? sixth of the relative minor; and as the interval between D-E, the major sixth and seventh, must be a 9-comma interval, and its own D-E is only an 8-comma one, it must take the D of A minor, which is a comma lower, and this will correctly show the 9-comma interval between D and E. This is the way of their mutual providing in the region of ?s; the ? sixth of the minor is given to be the ? fourth of the relative major; and the comma-lower fourth of the sub-relative minor becomes the correct sixth of the major. The arrows indicate the source from which, and the place to which; the new notes come and go. [Scientific Basis and Build of Music, page 113]

PLATE XIII.

THE VERTEBRAL COLUMN OF THE MUSICAL SCALE.

Major and Minor.

The Octave being divided into 53 commas, the intervals are measured, as usual, by these, the large second having 9-commas, the medium second having 8, and the small second 5. These measures are then made each the radius by which to draw hemispheres showing the various and comparative areas of the seconds. The comparative areas of the thirds are shown by the hemispheres of the seconds which compose them facing each other in pairs. The comma-measures of the various thirds thus determined are then made the radii by which to draw the two hemispheres of the fifths. The areas of the three fifths are identical, as also the attitudes of their unequal hemispheres. The attitude of the six thirds, on the other hand, in their two kinds, being reversed in the upper and under halves of the scale, their attitude gives them the appearance of being attracted towards the center of the tonic; while the attitude of the three fifths is all upward in the major, and all downward in the minor; their attraction being towards the common center of the twelve scales which Nature has placed between the second of the major and the fourth of the minor, as seen in the two D's of the dual genetic scale, - the two modes being thus seen, as it were, revolving [Scientific Basis and Build of Music, page 113]

PLATE XIV.

THE VERTEBRAL COLUMN IN MODULATION.

When Plate XIII. is divided up the middle of the column, as in Plate XIV., so as that one side may be slipped up a fifth, representing a new key one-fifth higher, its subdominant made to face the old tonic, the two new notes are then pictorially shown, the second being altered one comma and the seventh four commas. The key at this new and higher pitch is by Nature's unfailing care kept precisely in the same form as the first; and wherever the major scale is pitched, higher or lower, the form remains unaltered, all the intervals arranging themselves in the same order. The ear, and the voice obedient to it, carry Nature's measuring-rule in them, and the writing must use such marks as may truly represent this; hence the use of sharps, flats, and naturals; these, however, be it observed, are only marks in the writing; all is natural at any pitch in the scale itself. All this is equally true of the minor mode at various pitches. These two plates are only another and more pictorial way of showing what the stave and the signature are usually made to express. [Scientific Basis and Build of Music, page 114]

PLATE XV.

THE CHROMATIC SCALE AND THE CHROMATIC CHORDS.

One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]

PLATE XXVIII.

Fig. 1. - This figure shows the major and minor measured in commas and placed directly as they stand related, major and relative minor, the minor being set a minor third lower than the major. The interval between C and E in the minor is an 8-and-9-comma interval; between C and E in the major it is a 9-and-8-comma one. This difference arises from the minor D being a comma lower than the major D. In all the other intervals minor and major are the same. [Scientific Basis and Build of Music, page 120]

Sympathetic Vibratory Physics

Bridging Science and Spirituality

Search

Interval