"The science of numbers ought to be preferred as an acquisition before all others, because of its necessity and because of the great secrets and other mysteries which there are in the properties of numbers. All sciences partake of it, and it has need of none." - [Boethius]
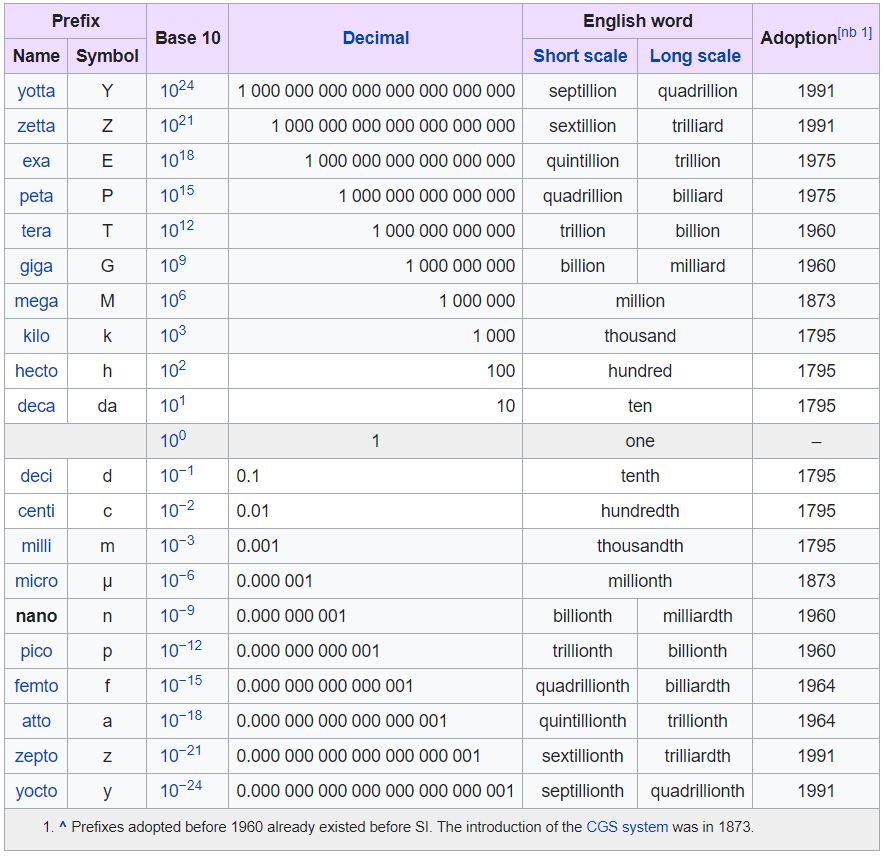
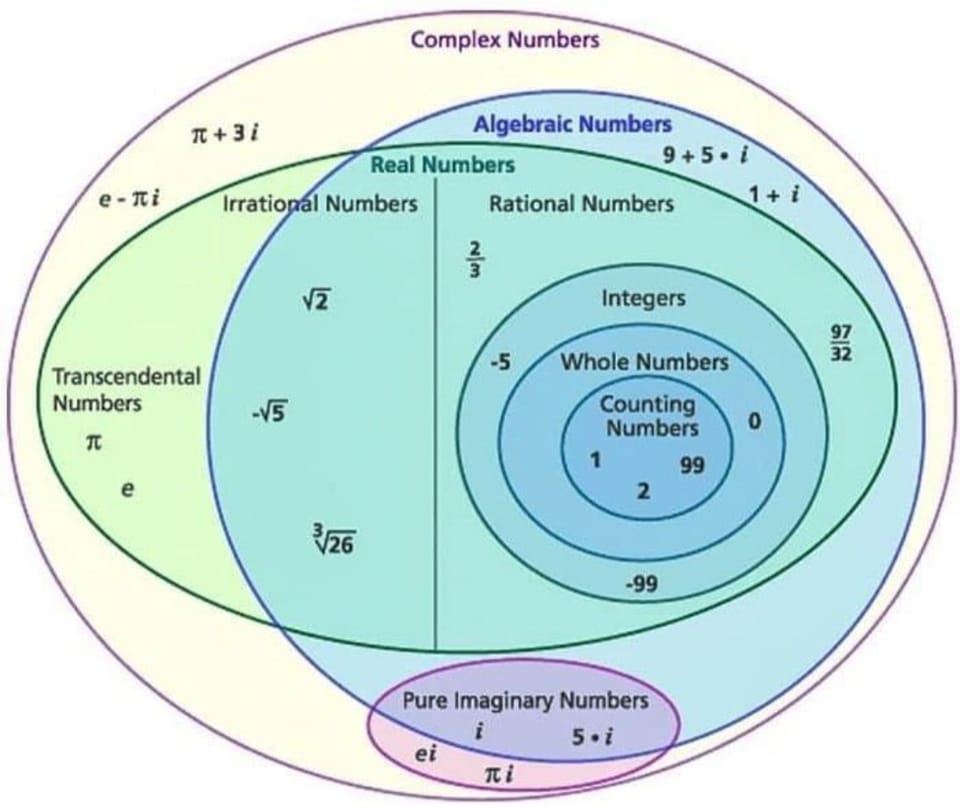
A number is a mathematical object used to quantify (count and measure) and to represent quantity, in several forms, of which the most primitive, primary and simplest one is the symbolic signification of a particular, invariable, constant quantity. A notational symbol that represents a number is called a numeral but in common use, the word number can mean the abstract object, the symbol, or the word for the number. In addition to their use in counting and measuring, numerals are often used for labels (telephone numbers), for ordering (serial numbers), and for codes (e.g., ISBNs). In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers.
Certain procedures that take one or more numbers as input and produce a number as output are called numerical operations. Unary operations take a single input number and produce a single output number. For example, the successor operation adds one to an integer, thus the successor of 4 is 5. More common are binary operations, which take two input numbers and produce a single output number. Examples of binary operations include addition, subtraction, multiplication, division, and exponentiation. The study of numerical operations is called arithmetic. [wikipedia]
The symbols for the digits 1 - 9 were derived from the ancient astrological symbols for the planets.
Where did numbers come from?
Keely
"The polar flow, as induced by the transmitter, is intensified or diminished by an oscillating bar which governs the revolutions to any number without variation." [The Operation of the Vibratory Circuit]
"He [Keely] has invented instruments which demonstrate in many variations the colours of sound, registering the number of necessary vibrations to produce each variation. The transmissive sympathetic chord of B flat, third octave, when passing into inaudibility, would induce billions of billions of vibrations, represented by sound colour on a screen illuminated from a solar ray." [Bloomfield-Moore] [3rd octave]
Schauberger
this energy-form is conducted into a glass bulb super-saturated with air containing oxygen, then about the same number of water-droplets appear as the seed-volts measured on the electrometer. With this we are already presented with the birth of water and the form of motion that induces it. [The Energy Evolution - Harnessing Free Energy from Nature, The Ennoblement of Water]
Ramsay
"...the things of the senses, will rejoice to find, at every step of the way in which music handles numbers, expressions of deep mysteries which are not discerned but by the spiritual sight." [Scientific Basis and Build of Music, page 21]
"The ratio of 1:2 is essentially simple in its character, and any power of the prime 2 always produces a note like itself. It is a law in musical science that doubling or halving a number never changes its character. Whatever ratios and notes are produced from the first power, the square, and the cube of any number, the same kind of ratios and notes will be produced, in the genesis of octaves, by the doubles or halves of that number. On this account the prime 2 has unlimited powers in producing notes, and is used in the first place in getting a series of octaves from 1 as unity;" [Scientific Basis and Build of Music, page 26]
of twelve mathematical scales is that F# and G?, which in the tempered system are one, being counted the same, are made two scales in the mathematical; but it is a needless nicety. Twelve is the natural number and period for both mathematical and tempered scales. And as the system of twelve Fifths contains the key system of music four times, only three of these twelve Fifths being required for any one key, it follows that the tempered key is affected by only one-fourth part of the small amount to be tempered into the whole twelve. [scientific Basis and Build of Music, page 30]
Well, how are we to get the true minor scale? There is a remarkable fact, and a beautiful one, which suggests the method. Such is the economy of Nature, that from one system of proportion employed in two different ways, in the one case as periods of vibrations and in the other as quantities of strings, everything in Music's foundation is produced. It is a remarkable fact that the numbers for the lengths of the strings producing the major scale are the numbers of the vibrations producing the minor scale; and the numbers for the lengths of the strings for the minor scale are the numbers of the vibrations of the notes of the major scale. Here Nature reveals to us an inverse process for the discovery of the minor scale of notes. [Scientific Basis and Build of Music, page 31]
A grave harmonic is a secondary note which spontaneously arises when two different notes are sounded together. It is a note whose mathematical number is the difference of the two which awaken it; e.g., F2 and C3, the interval of the fifth, awakens a grave harmonic whose number is 1, which is the difference of 2 and 3; and this 1 strengthens F2, for it is its lower octave. But the interval of F2 and F4, or any other octave, does not awaken a grave harmonic, since there is no difference-number between the two. - Editor. [Scientific Basis and Build of Music, page 36]
It is in their inverse relations that the major and the minor are equal. Every note, chord, and progression in the one has its reciprocal or corresponding note, chord, and progression in the other. This is the Law of Duality. And this general law of Nature is so deeply rooted in music, that is the numbers which represent the vibrations in the major system be made to represent quantities of string, these quantities will produce the minor system (beginning, of course, with the proper notes and numbers); so that when the quantities are minor the tones are major, and when the quantities are major the tones are minor.1[Scientific Basis and Build of Music, page 44]
Such is the economy of Nature, that from one system of proportions employed in two ways - in the one case as periods of vibrations, and in the other case as quantities of strings - everything in music is derived. The numbers which are the periods in the one are the numbers which are the quantities in the other. And abundantly throughout Creation reigneth the Law of Duality, which thus reigneth here in this region of most perfect response.2[Scientific Basis and Build of Music, page 44]
dividing itself by 2 or 3 or 5, etc., up through the whole geometrical series of numbers, not keeping fixed at one thing; but while the whole length is vibrating the fundamental partial, it keeps shifting the still nodes along its length, and sometimes longer and sometimes shorter segments are sounding the other partials which clothe the chief sound. It has been commonly said that "a musical sound is composed of three sounds," for every ear is capable of hearing these three, and with a little attention a few more than these; but many will be startled when told that there are twenty-five sounds in that sound. Eighteen of them are simply the octaves of the other seven, all of these seven except one having one or more octaves in the sound. Four of the seven also are very feeble, the one which has no octave being the feeblest of all. Two of the other three are so distinctly audible along with the chief partial that they gave rise to the saying we have quoted about a musical sound being composed of three sounds.1 If the three most pronounced partials were equally developed in one sound, it could not be called one sound - it would decidedly be a chord; and when in the system they do become developed, they form a chord; but in the one sound they, the partials, having fewer and fewer octaves to strengthen them, fade away in the perspective of sound. The sharp seventh, which in the developed system has only one place, not coming into existence until the sixth octave of the Genesis, is by far the feeblest of all the partials, and Nature did well to appoint it so. These harmonics are also sometimes called "overtones," because they are higher than the fundamental one, which is the sound among the sounds, as the Bible is the book among books. [Scientific Basis and Build of Music, page 59]
In getting the length of a string, in inches or otherwise, to produce the scale of music, any number may be fixed on for the unit; or for the vibrations of the root note any number may be fixed on for the unit; but in the fractions which show the proportions of the notes of the scale, there is no coming and going here; this belongs to the invariables; there is just one way of it. Whatever is not sense here is nonsense. It is here we are to look for the truth. The numbers which express the quantities and the numbers which express the motions are always related as being of the same kind. The fractions bring their characters with them, and we know by this where they come from. 1/4 of a string gives a note 2 octaves above the whole string, no matter what may be its length; 2 has exactly the same character as 1; 2/4 gives the note which is 1 octave above the whole string; but in the case of 3/4 here is a new ingredient, 3; 3/4 of a string gives a note which is a fifth below the [Scientific Basis and Build of Music, page 75]
There is nothing extraordinary in this. It is another fact which gives this one its importance, and that is that the musical system is composed of three fifths rising one out of another; so this note by 3/4 becomes the root not only of a chord, but the root of all the three chords, of which the middle one is the tonic; the chord of the balance of the system, the chord of the key; the one out of which it grows, and the one which grows out of it, being like the scales which sway on this central balance-beam. Thus F takes its place, C in the center, and G above. These are the 3 fifths of the system on its masculine or major side. The fractions for A, E, and B, the middle notes of the three chords, are 4/5, 3/5, and 8/15; this too tells a tale; 5 is a new ingredient; and as 3 gives fifths, 5 gives thirds. From these two primes, 3 and 5, along with the integer or unit, all the notes of the system are evolved, the octaves of all being always found by 2. When the whole system has been evolved, the numbers which are the lengths of the strings in the masculine or major mode are the numbers of the vibrations of the notes of the feminine or minor mode; and the string-length-numbers of the minor or feminine are the vibration-numbers of the notes of the major or masculine mode. These two numbers, the one for lengths and one for vibrations, when multiplied into each other, make in every case 720; the octave of 360, the number of the degrees of the circle. [Scientific Basis and Build of Music, page 76]
pendulum where fourth the length is double the oscillations. A third condition in this order is in springs or reeds where half the length is four times the vibrations. If we take a piece of straight wire and make it oscillate as a pendulum, one-fourth will give double the oscillations; if we fix it at one end, and make it vibrate as a spring, half the length will give four times the vibrations; if we fix it at both ends, and make it vibrate as a musical string, half the length will produce double the number of vibrations per second. [Scientific Basis and Build of Music, page 80]
The sympathy of one thing with another, and of one part of a thing with another part of it, arises from the principle of unity. For example, a string requires to be uniform and homogenous to have harmonics producing a fine quality of tone by the sweet blendings of sympathy; if it be not so, the tone may be miserable ... You say you wish I were in touch with Mr. Keely; so do I myself ... I look upon numbers very much as being the language which tells out the doings of Nature. Mr. Keely begins with sounds, whose vibrations can be known and registered. I presume that the laws of ratio, position, duality, and continuity, all the laws which go to mould the plastic air by elastic bodies into the sweetness of music, as we find them operative in the low silence of oscillating pendulums, will also be found ruling and determining all in the high silence of interior vibrations which hold together or shake asunder the combinations which we call atoms and ultimate elements, but which may really be buildings of wondrous complexity occupying different ranges of place and purpose between the visible cosmos and Him who built and evermore buildeth all things. The same laws, though operating in different spheres, make the likenesses of things in motion greater than the differences. [Scientific Basis and Build of Music, page 87]
It is a remarkable fact that the numbers for the lengths of strings producing the major scale are the number of the vibration of the notes of the minor scale; for example, string-length as 26 2/3 will give the vibrations for [Scientific Basis and Build of Music, page 87]
Whatever interval is sharpened above the tone of the open string, divide the string into the number of parts expressed by the larger number of the ratio of the interval, and operate in that part of the string expressed by the smaller number of it. For example, if we want to get the major third, which is in the ratio of 4:5, divide the string into five parts and operate on four. The lengths are inversely proportional to the vibrations. [Scientific Basis and Build of Music, page 100]
THIS plate is a Pendulum illustration of the System of musical vibrations. The circular lines represent Octaves in music. The thick are the octave lines of the fundamental note; and the thin lines between them are lines of the other six notes of the octave. The notes are all on lines only, not lines and spaces. The black dots arranged in these lines are not notes, but pendulum oscillations, which have the same ratios in their slow way as the vibrations of sounding instruments in the much quicker region where they exist. The center circle is the Root of the System; it represents F1, the root of the subdominant chord; the second thick line is F2, its octave; and all the thick lines are the rising octaves of F, namely 4, 8, 16, 32, and 64. In the second octave on the fifth line are dots for the three oscillations which represent the note C3, the Fifth to F2, standing in the ratio of 3 to 2; and the corresponding lines in the four succeeding Octaves are the Octaves of C3, namely 6, 12, 24, and 48. On the third line in the third Octave are 5 dots, which are the 5 oscillations of a pendulum tuned to swing 5 to 4 of the F close below; and it represents A5, which is the Third of F4 among musical vibrations. On the first line in the fourth Octave are 9 dots. These again represent G9, which stands related to C3 as C3 stands to F1. On the seventh line of the same octave are 15 dots; these represent the vibrations of E15, which stands related to C3 as A5 stands to F1. On the sixth line of the fifth Octave are 27 dots, representing D27, which stands related to G9 as G9 stands to C3, and C3 also to F1; it is the Fifth to G. And last of all, on the fourth line of the sixth Octave are 45 dots, representing B45, which, lastly, stands related to G9 as E15 stands to C3, and A5 to F1; it is the Third to this third chord - G, B, D. The notes which arise in each octave coming outward from the center are repeated in a double number of dots in the following Octaves; A5 appears as 10, 20, and 40; G9 appears as 18 and 36; E15 appears as 30 and 60; D27 appears as 54; and last of all B45 only appears this once. This we have represented by pendulum oscillations, which we can follow with the eye, the three chords of the musical system, F, A, C; C, E, G; and G, B, D. C3 is from F1 multiplied by 3; G9 is from C3 multiplied by 3; these are the three Roots of the three Chords. Their Middles, that is their Thirds, are similarly developed; A is from F1 multiplied by 5; E15 is from C3 multiplied by 5; B45 is from G9 multiplied by 5. The primes 3 and 5 beget all the new notes, the Fifths and the Thirds; and the prime 2 repeats them all in Octaves to any extent. [Scientific Basis and Build of Music, page 102]
When Leonhard Euler, the distinguished mathematician of the eighteenth century, wrote his essay on a New Theory of Music, Fuss remarks - "It has no great success, as it contained too much geometry for musicians, and too much music for geometers." There was a reason which Fuss was not seemingly able to observe, namely, that while it had hold of some very precious musical truth it also put forth some error, and error is always a hindrance to true progress. Euler did good service, however. In his letters to a German Princess on his theory of music he showed the true use of the mathematical primes 2, 3, and 5, but debarred the use of 7, saying, "Were we to introduce the number 7, the tones of an octave would be increased." It was wise in the great mathematician to hold his hand from adding other notes. It is always dangerous to offer strange fire on the altar. He very clearly set forth that while 2 has an unlimited use in producing Octaves, 3 must be limited to its use 3 times in producing Fifths. This was right, for in producing a fourth Fifth it is not a Fifth for the scale. But Euler erred in attempting to generate the semitonic scale of 12 notes by the use of the power of 5 a second time on the original materials. It produces F# right enough; for D27 by 5 gives 135, which is the number for F#. D27 is the note by which F# is produced, because D is right for this process in its unaltered condition. But when Euler proceeds further to use the prime 5 on the middles, A, E, and B, and F#, in their original and unaltered state, he quite errs, and produces all the sharpened notes too low. C# for the key of D is not got by applying 5 to A40, as it is in its birthplace; A40 has already been altered for the key of G by a comma, and is A40 1/2 before it is used for producing its third; it is A40 1/2 that, multiplied by 5, gives C#202 1/2, not C200, as Euler makes C#. Things are in the same condition with E before G# is wanted for the key of A. G# is found by 5 applied to E; not E in its original and unaltered state, E30; but as already raised a comma for the key of D, E30 3/8; so G# is not 300, as Euler has it, but 303 3/4. Euler next, by the same erroneous methods, proceeds to generate D# from B45, its birthplace number; but before D# is wanted for the key of E, B has been raised a comma, and is no longer B45, but B45 9/16, and this multiplied by 5 gives D#227 13/16, not D225, as Euler gives it. The last semitone which he generates to complete his 12 semitones is B?; that is A#, properly speaking, for this series, and he generates it from F#135; but this already altered note, before A# is wanted for the key of B, has been again raised a comma [Scientific Basis and Build of Music, page 107]
ratio of 5:8; three, 3:5; and one, 16:27. There are seven fifths - one in the ratio of 45:64; one, 27:40; and five, 2:3; and seven corresponding fourths - five in the ratio 3:4; one, 40:54; and one 32:45. These are the ratios of the intervals in their simplest expressions as given in the second outer space above the staff in the plate. In the outer space the intervals are given less exactly, but more appreciable, in commas. The ratios of the vibration-numbers of each interval in particular, counting from C24, are given in the inner space above the staff. These vibration-numbers, however, are not given in concert pitch of the notes, but as they arise in the low audible region into which we first come in the Genesis from F1, in the usual way of this work. The ratios would be the same at concert pitch; Nature gives the numbers true at whatever pitch in the audible range, or in the low and high silences which lies out of earshot in our present mortal condition. [Scientific Basis and Build of Music, page 110]
It is very interesting to observe how the number seven, which is excluded from the Genesis of the system of vibration, comes into view after the Genesis is completed, not only in the seven seconds of the melodic scale, but also in the seven of each of the intervals. As there are seven days in the week, though the seventh was only after the genesis of creation was finished, so there are six intervals, but seven of each, as we have seen; and in each 7-fold group three magnitudes determined by the three genetic magnitudes of the seconds. There is much symbolic meaning in all this. Any of the intervals may be used in melody; in harmony also, either in simple or compound chords, they all have the honor of fulfilling a part; and even those, such as seconds and sevenths, which are less honorable in themselves, have great honor in compound chords, such as dominant sevenths and compound tonics, which fulfill exceedingly interesting functions in the society of chords. [Scientific Basis and Build of Music, page 110]
One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]
The middle portion with the zigzag and perpendicular lines are the chromatic chords, as it were arpeggio'd. They are shown 5-fold, and have their major form from the right side, and their minor form from the left. In the column on the right they are seen in resolution, in their primary and fullest manner, with the 12 minors. The reason why there are 13 scales, though called the 12, is that F# is one scale and G? another on the major side; and D# and E? separated the same way on the minor side. Twelve, however, is the natural number for the mathematical scales as well as the tempered ones. But as the mathematical scales roll on in cycles, F# is mathematically the first of a new cycle, and all the notes of the scale of F# are a comma and the apotome minor higher than G?. And so also it is on the minor side, D# is a comma and the apotome higher than E?. These two thirteenth keys are therefore simply a repetition of the two first; a fourteenth would be a repetition of the second; and so on all through till a second cycle of twelve would be completed; and the thirteenth to it would be just the first of a third cycle a comma and the apotome minor higher than the second, and so on ad infinitum. In the tempered scales F# and G? on the major side are made one; and D# and E? on the minor side the same; and the circle of the twelve is closed. This is the explanation of the thirteen in any of the plates being called twelve. The perpendicular lines join identical notes with diverse names. The zigzag lines thread the rising Fifths which constitute the chromatic chords under diverse names, and these chords are then seen in stave-notation, or the major and minor sides opposites. The system of the Secondary and Tertiary manner of resolution might be shown in the same way, thus exhibiting 72 resolutions into Tonic chords. But the Chromatic chord can also be used to resolve to the Subdominant and Dominant chords of each of these 24 keys, which will exhibit 48 more chromatic resolutions; and resolving into the 48 chords in the primary, secondary, and tertiary manners, will make 144 resolutions, which with 72 above make 216 resolutions. These have been worked out by our author in the Common Notation, in a variety of positions and inversions, and may be published, perhaps, in a second edition of this work, or in a practical work by themselves. [Scientific Basis and Build of Music, page 115]
This is a twofold mathematical table of the masculine and feminine modes of the twelve scales, the so-called major and relative minor. The minor is set a minor third below the major in every pair, so that the figures in which they are the same may be beside each other; and in this arrangement, in the fourth column in which the figures of the major second stand over the minor fourth, is shown in each pair the sexual note, the minor being always a comma lower than the major. An index finger points to this distinctive note. The note, however, which is here seen as the distinction of the feminine mode, is found in the sixth of the preceding masculine scale in every case, except in the first, where the note is D26 2/3. D is the Fourth of the octave scale of A minor, and the Second of the octave scale of C major. It is only on this note that the two modes differ; the major Second and the minor Fourth are the sexual notes in which each is itself, and not the other. Down this column of seconds and fourths will be seen this sexual distinction through all the twelve scales, they being in this table wholly developed upward by sharps. The minor is always left this comma behind by the comma-advance of the major. The major A in the key of C is 40, but in the key of G it has been advanced to 40 1/2; while in the key of E, this relative minor to G, the A is still 40, a comma lower, and thus it is all the way through the relative scales. This note is found by her own downward Genesis from B, the top of the feminine dominant. But it will be remembered that this same B is the middle of the dominant of the masculine, and so the whole feminine mode is seen to be not a terminal, but a lateral outgrowth from the masculine. Compare Plate II., where the whole twofold yet continuous Genesis is seen. The mathematical numbers in which the vibration-ratios are expressed are not those of concert pitch, but those in which they appear in the genesis of the scale which begins from F1, for the sake of having the simplest expression of numbers; and it is this series of numbers which is used, for the most part, in this work. It must not be supposed, however, by the young student that there is any necessity for this arrangement. The unit from which to begin may be any number; it may, if he chooses, be the concert-pitch-number of F. But let him take good heed that when he has decided what his unit will be there is no more coming and going, no more choosing by him; Nature comes in [Scientific Basis and Build of Music, page 117]
with her irrevocable proportions to measure his scales for him. The stars at the C of the first scale and at the B# of the last show the coincidence of 12 fifths and 7 octaves. The number of B# is 3113 467/512; C24 multiplied 7 times by 2 brings us to the number 3072; these two notes in the tempered system are made one, and the unbroken horizon of the musical world of twelve twofold keys is created. The very small difference between these two pitches is so distributed in the 12 tempered scales that no single key of the 12 has much to bear in the loss of perfect intonation. [Scientific Basis and Build of Music, page 118]
This plate sets forth the essential duality of the musical system of vibrations. It is a remarkable fact that the numbers of the vibrations of the major mode are the numbers for the string proportions of the minor mode; and vice versa, the string proportions in the major are the numbers of the vibrations in the minor. We have, however, to see that we use the proper notes and numbers; we must know the secret of Nature. This secret rests in the duality of the notes, and begins from the two D's. The center of gravity of the musical system of vibrations is found in the comma space between the |two D's as they are found in the Genesis of the two modes. In these |two D's the vibration number and string proportions are nearly identical. Starting from this point as the center of gravity in the [Scientific Basis and Build of Music, page 118]
Another remarkable thing is that these dual numbers, when multiplied into each other, always come to 720. Now this number, as we see in the great Genesis, corresponds to 1 in the major, being the point of departure for the development of the feminine mode, as 1 is the point of departure in the masculine mode. This 720 is the octave of 360, which is the number of the degrees of the circle, so divided in the hidden depths of human antiquity; and when F1 becomes F2, then B360 is the answering note and number in the dual system. All the notes in the masculine development are above F2; and all the notes in the feminine development are below B360. The unoccupied octave between F1 and F2 and that between B720 and B360 may be counted as the octave heads or roots of the two modes, and then F2 and B360 as the points from which the development of music's diversity begins; and it is noteworthy that the number of the degrees of the circle should be found in this connection. When was the circle so divided? Who divided it so? And why did he, the unknown, so divide it? Was Music's mystery known in that far-off day before the confusion of man's sinking history had blotted out so much of the pure knowledge of pristine days? [Scientific Basis and Build of Music, page 119]
The inner stave contains the chromatic scale of twelve notes as played on keyed instruments. The flat and sharp phase of the intermediate notes are both given to indicate their relation to each other; the sharpened note being always the higher one, although seemingly on the stave the lower one. The two notes are the apotome minor apart overlapping each other by so much; ?D is the apotome lower than C#; ?E the apotome lower than D#; F# the apotome higher than ?G; G# the apotome higher than ?A; and A# the apotome higher than ?B. The figures for the chromatic scale are only given for the notes and their sharps; but in the mathematical series of notes the numbers are all given. [Scientific Basis and Build of Music, page 120]
Hughes
The scheme endeavours to prove that the development of harmonies of sound and of colours is regulated by the law of Evolution as gained from the Scriptures
—Youthful impressions regarding my great-uncle Dr. Darwin's views
—My cousin Charles Darwin's views touched upon
—The scheme involves the belief that life developing from the Almighty is the general
key to disentangle the intricacies of the Natural Sciences
—A remark of Sir John Lubbock's quoted
—The development of Numbers, the stream of Time, the Sevens of Creation, &c., may eventually be proved to proceed by the same laws, . . . . . . . 9 [Harmonies of Tones and Colours, Table of Contents1 - Harmonies]
General remarks on harmonies of tones and colours
—The scheme gained without technical knowledge
—Brief explanation of how the laws were gained
—The development of numbers showed the "to and fro" in the development of sounds
—Multequivalency of harmonies veering round, or advancing and retiring in musical clef
—Before judging, close examination requested, . 12 [Harmonies of Tones and Colours, Table of Contents1 - Harmonies]
Helmholtz's experiments on developing colours shown to agree with the scheme
—The sounds of the Falls of Niagara are in triplets or trinities
—The Arabian system divides tones into thirds
—Two trinities springing from unity apparently the germ of never-ending developments in tones and colours
—Inequality of the equinoctial points; is the want of equilibrium the motive power of the entire universe?
—The double tones of keyed instruments, the meetings by fifths, the major and minor keys, so agree with the development of colours, that a correct eye would detect errors in a piece of coloured music
—Numbers not entered upon, but develope by the same laws
—Bass notes omitted in order to simplify the scheme, 18 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]
If health is still granted to me, and if an interest is created on the subject of these pages, I shall endeavour to explain by what means I gained the laws here described, and to enter upon the development of numbers as showing the stream of time ever falling into infinity, and gliding onwards; also the sevens in creation, with several other branches of the subject which are here untouched, or but briefly alluded to. It is my earnest desire that all may be closely examined. Indifference will grieve me, but even severe criticism will afford me pleasure, as proving that the subject is considered worthy of investigation. [Harmonies of Tones and Colours, Introduction2 - Harmonies, page 10]
I had for a long time studied the development of the harmonics of colour, and believed that I had gained them correctly; but I saw no way of proving this. The thought occurred—Why not test the laws in musical harmonies? I wrote down the development of the seven major keys of the white notes in keyed instruments. I was perplexed by the movement as of "to and fro," but the development of numbers explained this point, and I found that the method of development in colours, tones, and numbers agreed. I remembered the keys with sharps, but had forgotten that B? belonged to the key of F, and here I thought that the laws failed. But I found by reference that all were correct, the eighth being the first of a higher series, the laws having enabled me to distinguish between flats and sharps, [Harmonies of Tones and Colours, General Remarks on Harmonies of Tones and Colours, page 12]
The development into triplets or trinities has been especially remarked in the harmony caused by the falls of Niagara.* "A remarkable peculiarity in the Arabian system of music is the division of tones into thirds. I have heard Egyptian musicians urge against the European systems of music that they are deficient in the number of sounds. These small and delicate gradations of sound give a peculiar softness to the performances of the Arab musicians." [Harmonies of Tones and Colours, The Arabian System of Music, page 21]
The inequality of the equinoctial points is a well-known fact. It will be seen how apparent this is in the developments of harmonies. From the moment that trinities depart from unity, the balance is unequal, and the repeated endeavours after closer union cause a perpetual restlessness. May not this want of equilibrium be the life or motive power of the entire universe, with its continuous struggle after concord, even to oneness? "Closer and closer union is the soul of perfect harmony." In tracing harmonies of tones and colours, the double tones of keyed instruments will be seen to correspond with the intermediate tints and shades of colours. The twelve notes, scales, and chords in the major and minor series, the meetings by fifths, &c., all agree so exactly in their mode of development, that if a piece of music is written correctly in colours with the intermediate tints and shades, the experienced musician can, as a rule, detect errors more quickly and surely with the eye than the ear, and the correct eye, even of a non-musical person, may detect technical errors. Although the arithmetical relation has been most useful in gaining the laws, it is not here entered upon; but numbers equally meet all the intricacies both of tones and colours. The bass notes have been omitted, in order to simplify the scheme. [Harmonies of Tones and Colours, The Arabian System of Music, page 21]
The keys of C and G meeting are coloured, and show the beautiful results of colours arising from gradual progression when meeting by fifths. Each key-note and its trinities have been traced as complete in itself, and all knit into each other, the seven of each rising a tone and developing seven times through seven octaves, the keys mingled. The twelve scales have been traced, developing seven times through seven octaves, all knit into each other and into the key-notes and their trinities. The chords have also been traced, each complete in itself, and all knit into each other and into the key-notes, trinities, and scales. And lastly, one series of the twelve keys, no longer mingled, but modulating into each other, have been traced, closely linked into each other by fifths through seven octaves, three keys always meeting. Mark the number of notes thus linked together, and endeavour to imagine this number of tones meeting from the various notes. [Harmonies of Tones and Colours, The Twelve Scales Meeting by Fifths, page 31a]
1867.—"Your plan of eliciting facts from Scripture (altogether new) interests me exceedingly." "To make out the scheme of harmonical parallel proper for the elucidation of your system, it will, if possible, run all true with the harmony of colour, and this has never yet been done, except in a way which has been met with serious objections. When I commenced the examination of your theory, I spent five days at the British Museum, and collated about forty volumes." "I am very glad to hear you have a probability of harmonising numbers by the same laws as light and sound." "What you call rest, I call the appearance and disappearance of a harmonical cycle." "Your series of fifths is quite correct." [Harmonies of Tones and Colours, Extracts from Dr. Gauntlett's Letters1, page 48]
1872.—"It gives me great pleasure to write to you on this subject. Music deals more with the imaginative faculty than any other art or science, and possessing, as it does, the power of affecting life, and making great multitudes feel as one, may have more than ordinary sympathy with the laws you work upon. You say 'from E, root of B, the fountain key-note F, root of C, rises.' There is a singular analogy here in the relativities of sounds, as traced by comparing the numbers made together by vibrations of strings with the length of strings themselves, the one is the inverse or the counterchange of the other. The length of B and E are the counterchange of F and C, hence they are twin sounds in harmony." [Harmonies of Tones and Colours, Extracts from Dr. Gauntlett's Letters1, page 48]
R. A. Schwaller de Lubicz
"Proportion belongs to geometry and harmony, measurement to the object and to arithmetic; and one necessitates the other. Proportion is the comparison of sizes; harmony is the relationship to measures; geometry is the function of numbers." [R. A. Schwaller de Lubicz, The Temple in Man, page 61]
"In fact, each of these individual members of the vegetable kingdom belongs to a genus, and this genus to a family; and these families belong to an original "lineage." At the head of this lineage is a Neter, a "Principle" synthesizing all the characteristics of this lineage; its number, its rhythm, its classification in the general harmony." [R. A. Schwaller de Lubicz, The Temple in Man, page 63]
Claude Bragdon
"Number is the within of all things, the “first form of Brahman.” It is the measure of time and space; it lurks in the heart beat and is blazoned upon the starred canopy of night." [Claude Bragdon (1866-1946), Theosophy and Architecture]
Rudolf Steiner
"Numbers can give you a clue to what is called meditation if you have the key to plunge deeply enough." [Rudolf Steiner, Nov 15, 1907, Stuttgart]
See Also
Addition
Arithmetic
atomic number
Base 10
Base 12
Chord
Delta
Division
Eight
Figure 3.00 - Infinite Number of Atomoles or Alphanon filling all Space
Five
Four
Geometry
Indig Numbers
Integer
Interval
law of multiple proportions
law of constant composition
Law of Definite Proportions
mass number
Measure
Multiplication
Music
Nine
One
order of numbers
Oxidation Number
Pico Technology
proton number
Proportion
Propositions of Geometry
Quantum Arithmetic
Ratio
Scientific Notation
Seven
Six
Stoichiometry
Subtraction
Three
Two
unit of quantities
wave number
12.21 - Fibonacci Whole Numbers v Irrational Decimal near Equivalents
