Music: The Interval between a fundamental tone and the eighth step above it; all the tones within the Interval of an octave. Computed by doubling 2X or halving 1/2 establishes the octave in music (powers of 2) and diverse engineering fields. When Russell uses this term it usually refers to doubling or halving of VOLUME, Power or density (powers of 3).

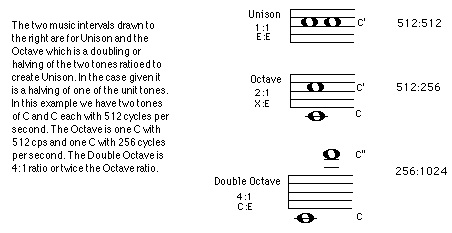
A doubling or halving. Usually applied to frequency, i.e., a gain rolloff rate of 6dB per octave for each doubling or halving of frequency. Power of 2.

(1) The Interval of an eighth. It may be major, minor, or augmented.
(2) The first note of the harmonic scale.
(3) An organ stop of 4 ft. pitch on the manuals, or 8 ft. on the pedals.
(4) The eight days following a great festival of the Church. [Dictionary of Music]

---

Walter Russell
When Russell uses this term he means the doubling and/or halving of the eighteen dimension quantities. In ordinary music comprised of frequencies the octave deals in doubling or halving in an arithmetic linear format. In the Russell use the octave is a doubling or halving of eighteen dimensions having a geometric format. [see Locked Potentials, Eighteen Attributes or Dimensions]

Distance, Area and Volume Ratios (courtesy University of Science and Philosophy) (click to enlarge)

Volume, Octave and Wave Structure (courtesy University of Science and Philosophy) (click to enlarge)

"In this Universe, the octaves of the elements of matter "Grow" from seed, just as all things grow from seed. Elements are not fixed created things. They are pressure conditions of light waves. The inert gases are the cosmic seeds of matter in this Universe. They surround the zero from which motion springs and to which it returns. They are the seeds of the octaves of matter, and each octave has a different seed just as different trees has different seeds. The inert gases are the recorders in cosmic seed of this creating universe of infinite continuity." [Russell]

"The master-tone of each octave is the inheritance of the original motion of the thinking process of Mind. These master-tones are the "inert gases" which are classified in the zero group of the Mendeleef table.

The state of motion of these inert gases is that of motion-in-inertia."

"Motion-in-inertia is that state of pressure equilibrium which lies between any two masses.

"The inertial line, or plane is that dividing line, or plane, toward which all masses discharge their potential.

"It is the line, or plane, of lowest potential of two opposing areas of potential, where opposing pressures neutralize. This is the plane of minimum pressure of two opposing areas.

"The master-tones which represent a state of motion-in-inertia and are the inert gases, bear the same relationship to the elements that white bears to the colors. They are a registration of them all. White is not included in the spectrum, it has no place there. The inert gases should not be included in the elements. They have no place there. Of this more shall be written later in its proper place." [Russell, The Universal One]

"The universe of matter is a registration of the energy expended by Mind in the effort of thinking. The exact energy of the action of thinking is registered in the electro-positive charging systems, and the reaction of the action is registered in the electro-negative discharging systems. The charging systems are electrically dominated, centripetally closing, contracting systems. The discharging systems are magnetically dominated, centrifugally opening, expanding systems. The low potential speed-time dimension of energy of the highest octave is gradually accumulated into the high potential power-time dimension of the fifth octave. When these two opposing dimensions equalize in the tenth octave the cycle is completed and begins again." [Figure 12.11 - Russells Locked Potential Full Ten Octave Gamut]

"Spheres occur only at wave amplitudes and the fact of its four positive and four negative efforts is the basis of the octave wave from which our spectrum, our octaves of the elements and our octaves of musical tones are derived.
"This 0, 1, 2, 3, 4, 4, 3, 2, 1, 0 octave sequence constitutes the heartbeat of the universe. It is the basis of our musical rhythms, our chemistry, our mathematics, our symmetry of design of all animal, mineral and vegetable forms and of our color spectrum of light." [Walter Russell, Home Study Course, 53 - Unit Nine - Lesson 35]

"The axis of the controlling plane of each elemental line has been extended to its opposing focal point and attached to its opposite element. This is indicated by rectangles in order to call attention to their parallel positions. The universal gyroscope assorts all states of motion by their planes of gyration. Like planes seek each other. The four tones of any octave exactly equal four tones of any other octave in mass energy. To crowd their accumulated forces into smaller volume does not in any way alter their energy." [Mathematical Relations are Constant]

THE OCTAVE NUMBERS
Charging systems are positive systems. Positive systems are male systems. Male systems are 1+2+ & 3+. Discharging systems are negative systems. Negative systems are female systems. Female systems are 1-2- & 3-. Number four is equally a charging system and a discharging system. It is a bi-sexual system. It is male-female. As the magnetic orbit of 4 is divided into two separate and opposing orbits, this maximum potential shall be doubly numbered as 4‡.
Two opposed tones = one unit.
Four units = one octave
Ten octaves = one cycle
+ THIS SYMBOL MEANS POSITIVE OR MALE.
- THIS SYMBOL MEANS NEGATIVE OR FEMALE.
‡ THIS SYMBOL MEANS EQUALLY MALE-FEMALE.
= THIS SYMBOL MEANS NEGATION. [Octave Numbers]

---

Tyndall
"The first octave is 6 1/4 times the fundamental when bowed, however, when struck, the 1st overtone is the octave, this octave being due to the secondary waves set up when the limits of the LAW OF SUPERPOSITION have been exceeded." [Tyndall, John; Sound; pg 381]

Ramsay
Euler, while treating of music, shows that there are just three mathematical primes, namely 2, 3, and 5, employed in the production of the musical notes - the first, in ratio of 2 to 1, producing Octaves; the second, in the ratio of 3 to 1, producing Fifths; and the third, in the ratio of 5 to 1, producing Thirds. [Scientific Basis and Build of Music, page 8]

"The system of musical sounds is derived from the laws of motion and a particular election of numbers which give the greatest variety of simple ratios. There are three primary and pregnant ratios which produce the chords and scales. The first is the ratio of 1:2, producing Octaves, and nothing else; the second is the ratio of 2:3, producing Fifths; the third is the ratio of 4:5, producing Thirds." [Scientific Basis and Build of Music, page 26]

"The ratio of 1:2 is essentially simple in its character, and any power of the prime 2 always produces a note like itself. It is a law in musical science that doubling or halving a number never changes its character. Whatever ratios and notes are produced from the first power, the square, and the cube of any number, the same kind of ratios and notes will be produced, in the genesis of octaves, by the doubles or halves of that number. On this account the prime 2 has unlimited powers in producing notes, and is used in the first place in getting a series of octaves from 1 as unity;" [Scientific Basis and Build of Music, page 26]

"notes which are produced by the two primes, 3 and 5. As the quadrant contains all the angles which give the different proportions in form, so does the ratio of 1:2, or the area of an octave, contain all the different notes in music. The ratio of 1:2 corresponds to unity, and, like the square and the circle in form, admits of no varieties. Half the length of a string gives an octave when the string is homogeneous and uniform; if the one half has more gravity than the other, the center of gravity of the whole string gives the octave. The ratio of 1:2 rests on the center of gravity. [Scientific Basis and Build of Music, page 27]

"The ratio of 2:3 twelve times, in Fifths, is so near the ratio of 1:2 seven times, in Octaves, as to allow this cycle of the mathematical scales to be closed without losing any of its vitality. The reason why there are thirteen instead " [Scientific Basis and Build of Music, page 29]

But let us proceed with our development, for we need another fifth, a lower one, a subdominant for our minor scale. Well, let us divide A5 by 3 and we have D1 2/3, the root of the lowest fifth; and if we divide A5 by 5 we have for our middle to this fifth F1, and this is F just as we find it at the major start, and identical in quantity in both major and minor. But let us examine the D1 2/3. It is not easy to compare D1 2/3 with D27 of the major; let us bring it up a few octaves by multiplying by 2. This will not alter its quantity, but simply give us the same quantity in a higher octave, in which we may more easily compare it with the major D1 2/3 multiplied by 2 is 3 1/3; multiplied again by 2 is 6 2/3; once more by 2 it is 13 1/3; and once more by 2 it is 26 2/3. Now we can compare it with D27 of the major, and we find this strange fact, that it is a little lower than the major D. The two D's are at the center of the dual system, but the center of the system is neither in the one D nor in the other, but as an invisible point between them, like the center of gravity in a double star; for the minor D is pushed a little below the center, and the major D is pushed a little above the center of the two modes of the system. [Scientific Basis and Build of Music, page 32]

Nature's own art, not man's device, enables us to realize and represent all the harmonic progressions that belong to music. It has been nature's self to the practical and inspired musician. By the division of the octave into twelve semitones, he is emancipated from the restrictions and jargon which arise from misapplied mathematics. The mathematicians say that such and such things are wrong; the great masters in music inspirationally do these very things. [Scientific Basis and Build of Music, page 33]

Either the one or the other must be at fault. Had the dictates of the mathematicians and the scale of mathematical intonation wholly ruled, the advent of the great masters would have been impossible. It was well said by one writing in The Choir - "Theory should be made from music, and not music from theory . . . the final judge of music is the Ear." The Great Masters are the exponent artists of what is true in the Science of Music, though it may differ from what has been taught by the merely mathematical-intonation advocates of music science. It should not be forgotten that the science of the mathematical theorists is one thing, and that of the composers is another. Schubert, Beethoven, Mozart, Haydin, Mendelssohn, and such inspired musicians, who walked in the liberty wherewith Nature made them free, are sufficient authority against the bondage of the one-law theorists who would tie us down to the mathematical command which comes from without, but who know nothing of the life within music which is the law unto itself.¹ With twelve divisions in the Octave, each note is adapted to serve in any capacity, and does serve in every capacity by turns. It is quite clear that this cannot be said of the mathematically perfect notes. And this is where it is seen that what is perfect in mathematical ratios becomes imperfect in the Musical System. Indeed, the mathematical intonation does not give a boundary within which to constitute a System at all, but goes off into never-ending cycles. In music, Nature begins by producing the Diatonic Octave of seven notes, derived by the mathematical ratios²; [Scientific Basis and Build of Music, page 34]

Twelve divisions in the Octave serve all the purposes of music. This is the master-stroke of Nature in putting so much into seemingly so little. Twelve is the most genial of all numbers; it is nature's representative of the social order in music. It is the manifold divisibility of twelve which makes the chromatic system in music possible. The equalized scale of twelve semitones in the octave and the chromatic system of music are indissolubly connected. With this the scale of mathematical intonation has neither part nor lot. The life-force of the notes from the law of position gives them a versatility which they could never have had from fixed ratios, however numerous. If the interval of the octave be excepted, there are no two notes together in a chord, nor succeeding each other in the octave scale, having the same amount of specific levity or gravity; consequently each note has an expression and [Scientific Basis and Build of Music, page 35]

character of its own. And as Nature has constituted them, these various forces all converge to the Center of the Tonic Chord, and, with the exception of the interval of the octave itself, the notes of the tempered scale being a little nearer each other than the mathematically perfect notes, these converging forces and this tempering mutually assist each other, and give a greater decision to the resolution of chords. [Scientific Basis and Build of Music, page 36]

Mathematicians have not recognized the life-power of the notes, and so they have misapplied their calculations, though these were perfect in themselves. Assuming the place of dictators, they say with an air of authority that, "strictly speaking, nothing could be more scientifically and musically untrue than the chromatic scale of twelve equal semitones as played on a tempered instrument; for in it, as in the diatonic scale, the same natural law prevails that no two tones of equal mathematical relations can melodically succeed each other." Saying that the same natural law prevails implies that they are reasoning from analogy; but in this assumption they are dictating to Nature. In a similar way they might assume that the interval of the octave, like the other intervals, should have a grave harmonic.² But the fact that the octave interval has not a [Scientific Basis and Build of Music, page 36]

A grave harmonic is a secondary note which spontaneously arises when two different notes are sounded together. It is a note whose mathematical number is the difference of the two which awaken it; e.g., F2 and C3, the interval of the fifth, awakens a grave harmonic whose number is 1, which is the difference of 2 and 3; and this 1 strengthens F2, for it is its lower octave. But the interval of F2 and F4, or any other octave, does not awaken a grave harmonic, since there is no difference-number between the two. - Editor. [Scientific Basis and Build of Music, page 36]

If the effects of notes and chords had depended entirely on their mathematical ratios, then the effect of the subdominant, tonic, and dominant would have been alike; for these three chords have exactly the same ratios. It is the law of position which gives the tonic chord its importance, and not any special ratios embodied in its structure. The ratio of 2 to 1 has a pure, unmixed, invariable character, always realized in the interval of the octave. The notes produced from 1 by the first, second, and third powers of 3 have different degrees of centrifugal force. The character of the notes produced by the first power of 5 depends on the character of the notes from which they are derived, namely, 1, 3, and 9. The final character of the notes and chords derived by the same ratios is determined by the amount of force which they have acquired from the way in which they have been derived, and from their position in the system; and no matter where these notes may afterwards be [Scientific Basis and Build of Music, page 37]

Nature has not finished when she has given us the Diatonic Scale of notes as first generated. In the diatonic scale, in ascending from C, the root of the tonic, the first step is an interval of 9 commas, supposing that we adopt the common division of the octave into 53 commas, which is the nearest practical measuring rule; the second step has 8 commas; the third has 5; the fourth has 9; the fifth has 8; the sixth has 9; and the seventh and last has 5 commas. So we have three steps of 9 commas, two steps of 8, and two of 5. The order of the steps in the major is 9, 8, 5, 9, 8, 9, 5. In the minor the magnitudes are the same, but the order is 9, 5, 8, 9, 5, 9, 8. So there are three magnitudes.¹ But Nature has an equalizing process in the course of her musical marshallings, in which these greater ones get cut down, and have to change places with the lesser, when her purpose requires them so to do. [Scientific Basis and Build of Music, page 47]

a minor third. So by adding the middle of the minor dominant, G, but made G#, that the third so produced may be a minor third, according to the nature of the chromatic chords, we have on this minor side of the chord G#, B, D, F, which we may call its minor form, inasmuch as the semitone of its second minor third is the one, B-C, which genetically arises in the minor genesis; and inasmuch as it has also received its supplemental G# from the minor dominant. How shall we find its complement on the other side? We have seen that D, the Janus-faced center of this triad, B, D, F, looks, as D27, toward the major also; it has already F in common with the major subdominant. The very next step is to the middle of this chord, A. Middles, we have just seen, are ever ready to accommodate themselves; and this minor third triad claims that A be flattened, for on this side also, though its major side, it must have a minor third; so by adding the middle of the major subdominant, A, but made A?, according to the nature of chromatic intervals, that this F-A? also may be a minor third; and now we have it as B, D, F, A?, which we may call its major form, inasmuch as the semitone of its minor third, E-F, is the one which genetically arises in the major genesis, and inasmuch as it has now received its supplemental A? from the major subdominant. This, then, is the chromatic chord in its native place, and in its native constitution; a 4-note chord, wholly of the minor thirds. It will be observed that it has now, in its two forms, divided the octave into minor thirds - 4 minor thirds, so it is very much at home anywhere in the octave; indeed it is at home everywhere - G#, B, D, F, A?. And as every diatonic common chord in music is constituted of materials found in the octave of notes, it cannot be far from a chromatic chord in some one of its forms. [Scientific Basis and Build of Music, page 55]

We have already seen that this new compound chord, the chromatic, like the dominant seventh and subdominant sixth, is a 4-note chord, and, like them, made up of minor thirds - they mostly so, this wholly so; and we have seen that this compound chord embraces the whole octave, cutting it into minor thirds -

And now we shall also see the chromatic chord system cutting the octave into semitones. If we follow this chromatic chord system out, we shall have the octave [Scientific Basis and Build of Music, page 55]

dividing itself by 2 or 3 or 5, etc., up through the whole geometrical series of numbers, not keeping fixed at one thing; but while the whole length is vibrating the fundamental partial, it keeps shifting the still nodes along its length, and sometimes longer and sometimes shorter segments are sounding the other partials which clothe the chief sound. It has been commonly said that "a musical sound is composed of three sounds," for every ear is capable of hearing these three, and with a little attention a few more than these; but many will be startled when told that there are twenty-five sounds in that sound. Eighteen of them are simply the octaves of the other seven, all of these seven except one having one or more octaves in the sound. Four of the seven also are very feeble, the one which has no octave being the feeblest of all. Two of the other three are so distinctly audible along with the chief partial that they gave rise to the saying we have quoted about a musical sound being composed of three sounds.¹ If the three most pronounced partials were equally developed in one sound, it could not be called one sound - it would decidedly be a chord; and when in the system they do become developed, they form a chord; but in the one sound they, the partials, having fewer and fewer octaves to strengthen them, fade away in the perspective of sound. The sharp seventh, which in the developed system has only one place, not coming into existence until the sixth octave of the genesis, is by far the feeblest of all the partials, and Nature did well to appoint it so. These harmonics are also sometimes called "overtones," because they are higher than the fundamental one, which is the sound among the sounds, as the Bible is the book among books. [Scientific Basis and Build of Music, page 59]

Speaking of acute harmonics Pole says - "The first six are the only ones usually considered to be of any practical importance, and it is rarely possible to distinguish more than 10 or 12."
Mercenne (French, 1636) says - "Every string produces 5 or more sounds at the same instant, the strongest of which is called the natural sound of the string, and alone is accustomed to be taken notice of; for the others are so feeble that they are only perceptible to delicate ears . . . not only the octave and fifteenth, but also the twelfth and major seventeenth are always heard; and over and above these I have perceived the twenty-third and ninth partial tones in the dying away of the natural sound."[Scientific Basis and Build of Music, page 59]

which seems to show that not only has one part of a vibrating string sympathy with another part of it so as to go into harmonic partials, as we have just seen, but as if the very air itself had sympathy with harmoniously vibrating strings; for Tartini observed that two harmonious sounds being produced and sustained as they can be, for example, by a strong bow on the violin, a third sound will be heard. Tartini's name for it was simply "a third sound." This is not an overtone, as Helmholtz has called the harmonic partials of one sounding string, but an undertone, because it is a "grave harmonic," away below the sounds of the two strings which awaken it. The subject of these undertones has been carefully studied since Tartini's day, and more insight has been obtained since we are now able to count and register the vibration of any musical sound. Helmholtz has called these third sounds of Tartini's "difference sounds," because when awakened by two strings, for example, the vibration-number of the third tone is the difference of the vibrations-numbers of the two tones which awaken it. The note C with vibration-number 512, and another C whose vibration-number is 256, the octave, awakened no third sound, because there is no difference between the two numbers - the one is just the doubled or halved; but if we take C256 and G381, its fifth, the difference number is 128; this being a low octave of C256, it has the effect of strengthening the upper one. Helmholtz found this to be the law of the third sound as to its producing, and the effect of it when produced. This third sound, mysteriously arising in the air through the sympathy it has with all concordant things, is another among many more suggestions that the whole Creation is measured and numbered to be in sympathy one part with another. The Creation is a universe. [Scientific Basis and Build of Music, page 60]

contrast. In the fifth, the ratio being 2:3, the excess of 3 above 2 is 1; this 1 bears a simple relation to both the notes which awaken it. The grave harmonic in this case gives the octave below the lower of the two sounds; 1 is an octave below 2. This is the simplest relation "a third sound" can have to the two which awaken it, and that is why the fifth has the smallest possible degree of contrast. The octave, the fifth, and the fourth may be reckoned as simple ratios; the major and minor thirds and their inversions as moderately complex; the second, which has the ratio of 9:10, and the major fourth F to B and its inversion, are very complex. [Scientific Basis and Build of Music, page 61]

In just such a manner, only by more obvious leaps, the middle of the dominant in the advancing major scales is raised a sharp - i.e., four commas. When D27, the dominant top of the key of C, is multiplied by 5, it generates F#135; so, taking it one octave lower, F64 in C major is F#67 1/2 in the key of G. C96 in the key of G is C#101 1/4 in the key of D; G72 in the key of D is G#151 7/8 in the key of A. And this raising of the middle of the dominant goes on through all the twelve major keys.[Scientific Basis and Build of Music, page 62]

lastly it is altered again and becomes, by the power of 3 once more, F#,#, and serves in four keys. But this carries us beyond the horizon of our musical world of twelve keys; for in B#, the top of the tonic E, we have reached our twelfth fifth, and it here coalesces with C of the seventh octave, and closes the circle. This is the way that all notes become alternately altered, either by commas and sharps in the upward genesis of scales, or by commas and flats in the downward genesis, by the alternate powers of 3 and 5. In the upward genesis in this illustration, notes by the power of 5 serve in three keys, and those by the power of 3 serve in four keys. In the minors it is just the inverse on this by the Law of Duality. But no note serves for more than either three or four keys, as the case may be. [Scientific Basis and Build of Music, page 63]

If we view the Diatonic scale from the standpoint of their harmonizing, it is the first five notes of the octave which are the natural scale. The eight notes of the octave form a compound scale. So, in this view, in the octave of notes we have before us two scales; and this is true in both major and minor modes after their own dual fashion. In each of these two diatonic modes, the major and the minor, there are two semitones; but there are only two semitones altogether in the twofold system. When the major is generated by itself it has them both; and when the minor is generated by itself it also has both; but when the major and the minor are generated simultaneously, or as one great dual outgrowth, while the major in the ascending genesis is producing the semitone E-F, the third and fourth of its octave scale, the minor responsively in the descending genesis is producing the semitone B-C, the second and third of its octave scale. In this view of them, therefore, the semitone E-F belongs genetically to the major, and B-C to the minor; and this claim is asserted in the major tonic chord C E G, in which its own semitone is [Scientific Basis and Build of Music, page 64]

embedded; and in the minor tonic chord A C E in the same way is embedded its own semitone; and in these chords they appear in their proper places as third and fourth, C, d, E f, G; and second and third, A, b C, d, E. It is these first five notes of the octave scale which in a very distinctive way constitute the natural scale, which can be harmonized consecutively in one manner. The octave is seen in this view to be a compound scale, inasmuch as a compounding method of harmonizing has to be resorted to in passing consecutively from the sixth to the seventh. Similar compounding has to be done in the minor as well.¹ [Scientific Basis and Build of Music, page 65]

where there stands an open door between the sixth and the seventh, these two having no note in common, it is easy and natural to slip out of the key into another, either in ascending the major or descending the minor octave; and in order to keep in the key, the two chords of these notes have to reach out to each other a helping hand, and compound in order to affiliate. This, however, by the law of sympathy and assimilation, which reigns in this happy, realm, they are always ready to do.¹ [Scientific Basis and Build of Music, page 66]

This great genetic scale, the all-producer, the all-container, extends over six octaves on each side; for it is not till high in the sixth octave we get B in the major, and it is not till low in the sixth octave that we get F in the minor. It is in the fifth octave, however, that the note which is the distinctive mark of the masculine and feminine modes is generated. D27 in the major, and D26 2/3 in the minor, distinguishes the sex of the modes, and shows which is the head and which the helpmeet in this happy family.² On the major side F, the root of the subdominant chord, that is the chord which is a fifth below the key-note C, is the root of all. This is the beginning of this creation. If we call the vibration-number of F one, for simplicity's sake, then F1 is multiplied by 3 and by 5, which natural process begets its fifth, C, and its third, A; this is the root, top, and middle of the first chord. From this top, C3, grows the next chord by the same natural process, multiplying by 3 and by 5; thus are produced the fifth and third of the second chord, G and E. From the top of this second chord grows the third and last chord, by the repetition of the same natural process; multiplying G9 by 3 and by 5 we [Scientific Basis and Build of Music, page 66]

Chords in a harmony are not at liberty to succeed each other in the way that single notes in a melody may. The notes in a melody may succeed in seconds, or they may succeed in larger intervals, any interval in the octave, even sometimes very effectively there may be a leap or fall of a whole octave. Chords cannot follow each other in this free way; they are under law, and must succeed accordingly. Their law is that they must be linked together either by having something in common in their elements, or have small intervals, semitonic progressions, between them. The former way, by notes in common, is the most usual way in diatonic succession of chords, the latter way, by semitonic progression, is a chief feature and charm in chromatic succession; but both in diatonic and chromatic progression of chords in harmony, notes in common and semitonic progression are usually found together. [Scientific Basis and Build of Music, page 68]

The Chromatic Scale is naturally the last to come into view, for it is not generated by a mathematical process at all. Chromatic intervals are indeed found in the scale as mathematically generated. The semitones between B-C and E-F are two chromatic intervals, and the chord which occurs between the major and the minor in the chord-scale when it begins with the minor mode is a chromatic chord, though in an uncompleted condition. But the making of the octave into a chromatic scale of twelve small or semi-tones, is the work of modulation from one key to another through the whole twelve keys in either the major or minor sphere; and this process is fully set forth in the pre-note to the chromatic treatise. [Scientific Basis and Build of Music, page 69]

The number of Chromatic Chords. Three chromatic chords exhaust the semitonic 12-foldness of the octave. The chromatic scale is a much more even thing than the diatonic; contrast is not its feature, and we may expect [Scientific Basis and Build of Music, page 72]

There is no one musical interval which is the perfect measuring rule for the others. But the octave has been divided into 53 parts called commas, and these commas are as near a commensurable rule as we need seek for measuring the musical intervals; always remembering that, strictly speaking, these intervals are incommensurable. The large second has 9 commas; the medium second has 8; and the small second 5; and all other intervals, being of course composed of some of these seconds, can be measured accordingly. Thus the comma, though not itself an interval of our musical system, is the handy and sufficiently perfect inch, let us call it, for practical purposes in music. [Scientific Basis and Build of Music, page 75]

In getting the length of a string, in inches or otherwise, to produce the scale of music, any number may be fixed on for the unit; or for the vibrations of the root note any number may be fixed on for the unit; but in the fractions which show the proportions of the notes of the scale, there is no coming and going here; this belongs to the invariables; there is just one way of it. Whatever is not sense here is nonsense. It is here we are to look for the truth. The numbers which express the quantities and the numbers which express the motions are always related as being of the same kind. The fractions bring their characters with them, and we know by this where they come from. 1/4 of a string gives a note 2 octaves above the whole string, no matter what may be its length; 2 has exactly the same character as 1; 2/4 gives the note which is 1 octave above the whole string; but in the case of 3/4 here is a new ingredient, 3; 3/4 of a string gives a note which is a fifth below the [Scientific Basis and Build of Music, page 75]

There is nothing extraordinary in this. It is another fact which gives this one its importance, and that is that the musical system is composed of three fifths rising one out of another; so this note by 3/4 becomes the root not only of a chord, but the root of all the three chords, of which the middle one is the tonic; the chord of the balance of the system, the chord of the key; the one out of which it grows, and the one which grows out of it, being like the scales which sway on this central balance-beam. Thus F takes its place, C in the center, and G above. These are the 3 fifths of the system on its masculine or major side. The fractions for A, E, and B, the middle notes of the three chords, are 4/5, 3/5, and 8/15; this too tells a tale; 5 is a new ingredient; and as 3 gives fifths, 5 gives thirds. From these two primes, 3 and 5, along with the integer or unit, all the notes of the system are evolved, the octaves of all being always found by 2. When the whole system has been evolved, the numbers which are the lengths of the strings in the masculine or major mode are the numbers of the vibrations of the notes of the feminine or minor mode; and the string-length-numbers of the minor or feminine are the vibration-numbers of the notes of the major or masculine mode. These two numbers, the one for lengths and one for vibrations, when multiplied into each other, make in every case 720; the octave of 360, the number of the degrees of the circle. [Scientific Basis and Build of Music, page 76]

The root of the subdominant is F, in the key of C major; and the top of the dominant is D. The difference between these two notes at the top and bottom of the chord-scale, is the quantity which two octaves is more than three fifths; it is the ratio of 27 to 30, a comma less than the minor third whose ratio is 5 to 6. [Scientific Basis and Build of Music, page 76]

Taking the seven notes of the octave, we have among them 42 intervals in all, without including the octave. When two notes are sounded together, [Scientific Basis and Build of Music, page 76]

the excess of the vibrations of the one note over the other makes one or more sounds which are called "grave harmonics;" e.g., in the interval of the fifth, in the ratio of 2:3, the excess of 3 over 2 is 1, so the grave harmonic is an octave below the lowest of the two notes, that is, the ratio of 1:2. This reinforces the lowest note, 2, and gives it a solid effect. In this way the octave is incorporated into the fifth, and unity with variety is combined with the law of continuity at the very threshold of harmony. In 32 of the 42 intervals the grave harmonics are notes which belong to the natural scale. In the 10 remaining intervals which have not the exact number of vibrations found anywhere in the natural scale, 6 of them are from the number 7, thus - 7, 7, 7, 21, 21, 35; the remaining 4 are from 11, 13, 13, and 19. [Scientific Basis and Build of Music, page 77]

The simple natural scale is the fifth; the compound natural scale is the octave; the harmony scale, or chord-scale, is the three fifths; the great genetic scale is six octaves; for, like the six creation days, it takes the six octaves to give birth to the elements of which the wondrous structure of our music is built up; the birthplace of B, the seventh of the octave scale, is the sixth octave of the great genetic scale. The area of the twelve major and twelve minor scales is twelve fifths or seven octaves, the twelfth fifth being a comma and the apotome minor in advance of the seventh octave. This is a quantity so small that it can be ignored in real music; and the two notes, say E# and F, joined to close the circle of this horizon of our music world. E# is the top of the twelfth fifth, and F is the top of the seventh octave; and they are practically, though not exactly mathematically, the same note. Illustrations of this will be found among the plates of this work. [Scientific Basis and Build of Music, page 79]

Having found the framework of the major scale by multiplying F1 three times by 3, find the framework of the minor by dividing three times by 3. But what shall we divide? Well, F1 is the unbegotten of the 25 notes of the great genetic scale; B45 is the last-born of the same scale. We multiply upward from F1 for the major; divide downward from B45 for the minor. Again, B45 is the middle of the top chord of the major system, a minor third below D, the top of that chord, and the top of the whole major chord-scale, so B is the relative minor to it. Now since the minor is to be seen as the INVERSE of the major, the whole process must be inverse. Divide instead of multiply! Divide from the top chord instead of multiply from the bottom chord. Divide from the top of the minor dominant instead of multiply from the root of the major subdominant. This will give the framework of the minor system, B45/3 = E15/3 = A5/3 = D1 2/3. But as 1 2/3 is not easily compared with D27 of the major, take a higher octave of B and divide from it. Two times B45 is B90, and two times B90 is B180, and two times B180 is B360, the number of the degrees of a circle, and two times B360 is B720; all these are simply octaves of B, and do not in the least alter the character of that note; now B720/3 is = E240/3 = A80/3 = D26 2/3. And now comparing D27 found from F1, and D26 2/3 found from B720, we see that while E240 is the same both ways, and also A80, yet D26 2/3 is a comma lower than D27. This is the note which is the center of the dual system, and it is itself a dual note befittingly. [Scientific Basis and Build of Music, page 81]

There are two octaves in the key of C, as it is called. Now for the scale of a fifth higher than C, that is G, multiply the top of the dominant, that is the highest note of the chord-scale, by 3 and by 5, and the two new notes for the scale of G will be found; the rest of the notes are the same mathematically as those of C. [Scientific Basis and Build of Music, page 82]

N.B. - The sharp comes here by the prime 5, and the comma by the prime 3. Now we have the key of G provided for;-

These are two octaves of the scale of G. G A B, which in the scale of C was an 8-9-comma third, must now take the place of C D E, which in C was a 9-6-comma [Scientific Basis and Build of Music, page 82]

When higher or lower octaves of any note or scale are wanted for convenience of comparison, multiply or divide by two, the octave-producer. [Scientific Basis and Build of Music, page 83]

There are 32 notes required for each octave for the 13 major and the 13 minor mathematical scales. These 32 notes are by the law of duality arranged symmetrically from D as a center upwards to G#, and downwards to A?. D itself serves for 2 of the 32 on the piano. The first black keys on each side of D serve for nominally 3 notes each = 6. The first white key above and the first below D serve for 2 notes each = 4. The second white key above and the second below serve each for 3 notes = 6. The second black keys above and below D serve each for 3 notes = 6. The third black key above D is G#, the third below is A?; this key, for it is one, serves for 2 of the 32. There is a comma of difference between D minor and D major. Six fifths below the minor D26 2/3 is A?, the root of the subdominant of the key of E? minor; and six fifths above the major D27 is G#, the top of the dominant of F# major. The difference between this minor A? and this major G# is two commas and [Scientific Basis and Build of Music, page 85]

"To say that I was surprised at what Mr. Keely has discovered would be saying very little indeed ... It would appear that there are three different spheres in which the laws of motion operate. 1 - The first is the one in which Nature plays her grand fugue on the silent harp of Pendulums. In one period of Nature's grand fugue, as illustrated by pendulums, there are 19 ratios in 25 circles of oscillations ranging over 6 octaves; but all in silence. [Scientific Basis and Build of Music, page 86]

Seven notes in the Octave are required for the major scale, e.g., the scale of C. All the notes of the relative minor A are the same as those of the scale of C major, with exception of D, its fourth in its Octave scale, and the root of its subdominant in its chord-scale; thus, one note, a comma lower for the D, gives the scale of A minor. [Scientific Basis and Build of Music, page 88]

notes each; that is, 24 new notes, which, with the seven original major notes and the one different minor note, make 32 in all; and 32 notes in the Octave are all that belong to 13 major and 13 minor mathematical scales.¹ [Scientific Basis and Build of Music, page 89]

In a musical air or harmony, i.e., when once a key has been instituted in the ear, all the various notes and chords seem animated and imbued with tendency and motion; and the center of attraction and repose is the tonic, i.e., the key-note or key-chord. The moving notes have certain leanings or attractions to other notes. These leanings are from two causes, local proximity and native affinity. The attraction of native affinity arises from the birth and kindred of the notes as seen in the six-octave genesis, and pertains to their harmonic combinations. The attraction of local proximity arises from the way the notes are marshalled compactly in the octave scale which appears at the head of the genesis, and pertains to their melodic succession. In this last scale the proximities are diverse; the 53 commas of the octave being so divided as to give larger and lesser distances between the notes; and of course the attraction of proximity is strongest between the nearest; a note will prefer to move 5 commas rather than 8 or 9 commas to find rest. Thus far PROXIMITY. [Scientific Basis and Build of Music, page 91]

"Dividing the octave into twelve semitones is a near approach to the mathematical quantities, and this saves the musical artist from errors in tone - at least to any extent; but it does not save from errors in judgment. In the case of G#, for example, not one of the reasons given for the use of the sharp seventh in the minor scale is a correct one. A touch of nature makes the world akin, and a touch of the Law of Duality balances everything in music." [Scientific Basis and Build of Music, page 99]

THIS plate is a Pendulum illustration of the System of musical vibrations. The circular lines represent Octaves in music. The thick are the octave lines of the fundamental note; and the thin lines between them are lines of the other six notes of the octave. The notes are all on lines only, not lines and spaces. The black dots arranged in these lines are not notes, but pendulum oscillations, which have the same ratios in their slow way as the vibrations of sounding instruments in the much quicker region where they exist. The center circle is the Root of the System; it represents F1, the root of the subdominant chord; the second thick line is F2, its octave; and all the thick lines are the rising octaves of F, namely 4, 8, 16, 32, and 64. In the second octave on the fifth line are dots for the three oscillations which represent the note C3, the Fifth to F2, standing in the ratio of 3 to 2; and the corresponding lines in the four succeeding Octaves are the Octaves of C3, namely 6, 12, 24, and 48. On the third line in the third Octave are 5 dots, which are the 5 oscillations of a pendulum tuned to swing 5 to 4 of the F close below; and it represents A5, which is the Third of F4 among musical vibrations. On the first line in the fourth Octave are 9 dots. These again represent G9, which stands related to C3 as C3 stands to F1. On the seventh line of the same octave are 15 dots; these represent the vibrations of E15, which stands related to C3 as A5 stands to F1. On the sixth line of the fifth Octave are 27 dots, representing D27, which stands related to G9 as G9 stands to C3, and C3 also to F1; it is the Fifth to G. And last of all, on the fourth line of the sixth Octave are 45 dots, representing B45, which, lastly, stands related to G9 as E15 stands to C3, and A5 to F1; it is the Third to this third chord - G, B, D. The notes which arise in each octave coming outward from the center are repeated in a double number of dots in the following Octaves; A5 appears as 10, 20, and 40; G9 appears as 18 and 36; E15 appears as 30 and 60; D27 appears as 54; and last of all B45 only appears this once. This we have represented by pendulum oscillations, which we can follow with the eye, the three chords of the musical system, F, A, C; C, E, G; and G, B, D. C3 is from F1 multiplied by 3; G9 is from C3 multiplied by 3; these are the three Roots of the three Chords. Their Middles, that is their Thirds, are similarly developed; A is from F1 multiplied by 5; E15 is from C3 multiplied by 5; B45 is from G9 multiplied by 5. The primes 3 and 5 beget all the new notes, the Fifths and the Thirds; and the prime 2 repeats them all in Octaves to any extent. [Scientific Basis and Build of Music, page 102]

When these representative dots are arranged on these six Octaves of lines, at regular distances marked out by the proportionate degrees of the circle, they present to the eye this beautiful symmetrical picture of the Diatonic System of Musical Vibrations. They represent all that mathematically belongs to Music. When the notes are strung [Scientific Basis and Build of Music, page 102]

together on radial lines from the center they appear grouped in various chords and combinations, dropping out and coming in in such succession as to constitute what Ramsay, whose genius was given to set this thus before us, calls "Nature's Grand Fugue." Beginning at F in the center at the top, and moving either to the right or to the left, after a run of 7 notes we have 4 consecutive Octaves, and then comes the Minor fifth, A-E, followed by the Major fifth, G-D; and this by another Major fifth, F-C; the combinations keep changing till at the quarter of the circle we come to F, A, C, E, G, a combination of the subdominant and tonic Major; and after another varied series of combinations we have at the half of the circle the elements of 2 minor chords, D, F, A and A, C, E, and one Major chord, C, E, G; at the third quarter we have a repetition of the first quarter group; and the various chords and combinations dropping out and coming in, fugue-like; finally we return to where we began, and end with the three-times-three chord, in which the whole 25 notes are struck together, and make that wondrous and restful close of this strange Fugue. No one can hear the thrice-threefold chord of this close and ever forget it; it is "the lost chord" found; and leads the saintly heart away to the Three in One who is the Lord of Hosts; Maker of Heaven and Earth, and all the host of them. [Scientific Basis and Build of Music, page 103]

In the lowest Fig. this framework is filled up with all the octaves of the notes found as in the top Fig., the major being evolved upward and the minor downward, and the two systems centered at the D's, which are shown a comma distant from each other. [Scientific Basis and Build of Music, page 103]

Fig. 1 - The pendulums in this illustration are suspended from points determined by the division of the Octave into Commas; the comma-measured chords of the Major key being S, 9, 8, 9, 5; T, 9, 8, 5, 9; D, 8, 9, 5, 9. The pendulums suspended from these points are tuned, as to length, to swing the mathematical ratios of the Diatonic scale. The longest pendulum is F, the chords being properly arranged with the subdominant, tonic, and dominant, the lowest, center, and upper chords respectively. Although in "Nature's Grand Fugue" there are 25 pendulums engaged, as will be seen by reference to it, yet for the area of a single key 13 pendulums, as here set forth, are all that are required. It will not fail to be observed that thus arranged, according to the law of the genesis of the scale, they form a beautiful curve, probably the curve of a falling projectile. It is an exceedingly interesting sight to watch the unfailing coincidences of the pendulums perfectly tuned, when started in pairs such as F4, A5, and C6; or started all together and seen in their manifold manner of working. The eye is then treated to a sight, in this solemn silent harp, of the order in which the vibrations of sounding instruments play their sweet coincidences on the drum of the delighted ear; and these two "art senses," the eye and the ear, keep good company. Fig. 2 is an illustration of the correct definition of a Pendulum Oscillation, as defined in this work. In watching the swinging pendulums, it will be observed that the coincidences [Scientific Basis and Build of Music, page 104]

save the octave, and made them into one, so that in its proximate meetings during its period it seems composed of the ratio 2:3 twelve times, and 3:4 seven times; twelve times 2 and seven times 3 are 45; twelve times 3 and seven times 4 are 64. This long period of 45 to 64 by its proximate meetings divided itself into 19 short periods, and oscillates between the ratios of 2:3 and 3:4 without ever being exactly the one or the other; the difference being always a very small ratio, and the excess of the one being always the deficiency of the other. This fifth, B to F, has been misnamed an "imperfect fifth." When these two notes in the ratio of 45:64 are heard together, the oscillating proximately within it of the two simple ratios gives this fifth a trembling mysterious sound. [Scientific Basis and Build of Music,page 106]

This plate is a representation of the area of a scale; the major scale, when viewed with the large hemisphere, lowest; the minor when viewed the reverse way. It is here pictorially shown that major and minor does not mean larger and smaller, for both modes occupy the same area, and have in their structure the same intervals, though standing in a different order. It is this difference in structural arrangement of the intervals which characterizes the one as masculine and the other as feminine, which are much preferable to the major and minor as distinctive names for the two modes. Each scale, in both its modes, has three Fifths - subdominant, tonic, and dominant. The middle fifth is the tonic, and its lowest note the key-note of the scale, or of any composition written in this scale. The 53 commas of the Octave are variously allotted in its seven notes - 3 of them have 9 commas, 2 have 8, and 2 have 5. The area of the scale, however, has much more than the octave; it is two octaves, all save the minor third D-F, and has 93 commas. This is the area alike of masculine and feminine modes. The two modes are here shown as directly related, as we might figuratively say, in their marriage relation. The law of Duality, which always emerges when the two modes are seen in their relationship, is here illustrated, and the dual notes are indicated by oblique lines across the pairs. [Scientific Basis and Build of Music, page 106]

When Leonhard Euler, the distinguished mathematician of the eighteenth century, wrote his essay on a New Theory of Music, Fuss remarks - "It has no great success, as it contained too much geometry for musicians, and too much music for geometers." There was a reason which Fuss was not seemingly able to observe, namely, that while it had hold of some very precious musical truth it also put forth some error, and error is always a hindrance to true progress. Euler did good service, however. In his letters to a German Princess on his theory of music he showed the true use of the mathematical primes 2, 3, and 5, but debarred the use of 7, saying, "Were we to introduce the number 7, the tones of an octave would be increased." It was wise in the great mathematician to hold his hand from adding other notes. It is always dangerous to offer strange fire on the altar. He very clearly set forth that while 2 has an unlimited use in producing Octaves, 3 must be limited to its use 3 times in producing Fifths. This was right, for in producing a fourth Fifth it is not a Fifth for the scale. But Euler erred in attempting to generate the semitonic scale of 12 notes by the use of the power of 5 a second time on the original materials. It produces F# right enough; for D27 by 5 gives 135, which is the number for F#. D27 is the note by which F# is produced, because D is right for this process in its unaltered condition. But when Euler proceeds further to use the prime 5 on the middles, A, E, and B, and F#, in their original and unaltered state, he quite errs, and produces all the sharpened notes too low. C# for the key of D is not got by applying 5 to A40, as it is in its birthplace; A40 has already been altered for the key of G by a comma, and is A40 1/2 before it is used for producing its third; it is A40 1/2 that, multiplied by 5, gives C#202 1/2, not C200, as Euler makes C#. Things are in the same condition with E before G# is wanted for the key of A. G# is found by 5 applied to E; not E in its original and unaltered state, E30; but as already raised a comma for the key of D, E30 3/8; so G# is not 300, as Euler has it, but 303 3/4. Euler next, by the same erroneous methods, proceeds to generate D# from B45, its birthplace number; but before D# is wanted for the key of E, B has been raised a comma, and is no longer B45, but B45 9/16, and this multiplied by 5 gives D#227 13/16, not D225, as Euler gives it. The last semitone which he generates to complete his 12 semitones is B?; that is A#, properly speaking, for this series, and he generates it from F#135; but this already altered note, before A# is wanted for the key of B, has been again raised a comma [Scientific Basis and Build of Music, page 107]

The Octave being divided into 53 commas, the intervals are measured, as usual, by these, the large second having 9-commas, the medium second having 8, and the small second 5. These measures are then made each the radius by which to draw hemispheres showing the various and comparative areas of the seconds. The comparative areas of the thirds are shown by the hemispheres of the seconds which compose them facing each other in pairs. The comma-measures of the various thirds thus determined are then made the radii by which to draw the two hemispheres of the fifths. The areas of the three fifths are identical, as also the attitudes of their unequal hemispheres. The attitude of the six thirds, on the other hand, in their two kinds, being reversed in the upper and under halves of the scale, their attitude gives them the appearance of being attracted towards the center of the tonic; while the attitude of the three fifths is all upward in the major, and all downward in the minor; their attraction being towards the common center of the twelve scales which Nature has placed between the second of the major and the fourth of the minor, as seen in the two D's of the dual genetic scale, - the two modes being thus seen, as it were, revolving [Scientific Basis and Build of Music, page 113]

One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]

In the festoons of ellipses the signatures are given in the usual conventional way, the major F having one flat and minor E having one sharp. The major and minor keys start from these respective points, and each successive semitone is made a new keynote of a major and a minor respectively; and each ellipse in the festoons having the key shown in its two forms; for example, in the major F, one flat, or E#, eleven sharps; in the minor E, one sharp, or F?, eleven flats. Thus is seen all the various ways that notes may be named. The four minor thirds which divide the octave may be followed from an ellipse by the curved lines on which the ellipses are hung; and these four always constitute a chromatic chord. [Scientific Basis and Build of Music, page 115]

Another remarkable thing is that these dual numbers, when multiplied into each other, always come to 720. Now this number, as we see in the great genesis, corresponds to 1 in the major, being the point of departure for the development of the feminine mode, as 1 is the point of departure in the masculine mode. This 720 is the octave of 360, which is the number of the degrees of the circle, so divided in the hidden depths of human antiquity; and when F1 becomes F2, then B360 is the answering note and number in the dual system. All the notes in the masculine development are above F2; and all the notes in the feminine development are below B360. The unoccupied octave between F1 and F2 and that between B720 and B360 may be counted as the octave heads or roots of the two modes, and then F2 and B360 as the points from which the development of music's diversity begins; and it is noteworthy that the number of the degrees of the circle should be found in this connection. When was the circle so divided? Who divided it so? And why did he, the unknown, so divide it? Was Music's mystery known in that far-off day before the confusion of man's sinking history had blotted out so much of the pure knowledge of pristine days? [Scientific Basis and Build of Music, page 119]

This plate, in the outer stave, has the 32 notes which arise with mathematical development of twelve scales in advancing fifths. The notes are marked with sharps, flats, and commas. The flats and commas of lowering are placed on the left of the notes, in the order in which they arise, reading them from the note downward; the sharps and commas of rising on the right, also reading from the note upward. The whole of these 32 notes are brought within the compass of an octave. [Scientific Basis and Build of Music, page 119]

---

Hughes
The chords
—The fourteen roots of the chords of the twelve major keys
—A threefold major chord examined, fourfold with its octave
—The seven of each key seen to have two chords and its scale one chord, thirty-six in all, forty-eight with octaves
—The chords of the twelve keys as they follow in order are written in musical clef
—Colours seen to agree, . . . 27 [Harmonies of Tones and Colours, Table of Contents2 - Harmonies]

whether veering round, or advancing and retreating in musical clef. I next tried the major keys which develope flats, and I thought that G? would develope a perfect harmony, but found that it must be F#, and that in this one harmony E# must be used in place of F?; on reference, I found that thus the twelve keys developed correctly in succession, the thirteenth being the octave, or first of a higher series. [Harmonies of Tones and Colours, Dr. Gauntletts Remarks1, page 13]

the artificial system must not be mixed up. The wonders of Nature's laws in the developments of harmonies, consist in the beautiful adaption of keyed and all other musical instruments to a range commensurate with human powers. The chromatic scale of twelve notes (the thirteenth being the octave) is not the scale of Nature. To construct a musical instrument upon real divisions of musical tones, each of them being in correct ratio with the others, it would be necessary to have a larger number of tones to the octave. In the development of harmonies on the natural system, we trace the perfect adaptation of means to ends, meeting the intricacies of every musical instrument, including that most perfect of all— the human voice. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies3, page 17]

If the laws which I shall endeavour to explain develope the twelve major harmonies, with each note in succession expanding its six tones from within itself; and if each of these is found to be a lower development, which leads the ear to a corresponding higher expansion of the twelve major key-notes, and the six tones of each ascending and descending in an unbroken sequence from any twelve consecutively, the thirteenth being the octave of the first, which commences a higher or a lower series; and if the twelve minor harmonies are also gained by the same laws from their twelve relative key-notes (the thirteenth again being octave): if, again, all other notes are shown to be but higher or lower repetitions of these twenty-four harmonies—may we not consider the problem as in some measure solved? especially as the harmonies proceed in geometric as well as harmonical ratio, and an accurate parallel can be traced between the development of notes and colours, which latter correspond with all the intricacies of harmonic sounds. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies3, page 17]

The diagram begins with C, the third space of the treble clef, as being more convenient to write than C, the lowest note in the bass clef. The life of musical sounds rising from a hidden fountain of life is shown by the chasms of keyed instruments between B and C, and E and F; their great use will be strikingly manifest as the developments proceed. The fundamental key-note C and its root F rise from the chasms. B, the twelfth key-note, and E, its root, sound the octave higher of the fountain B. The generation of harmonies is by one law a simple mode of difference. Each major major key-note and its tones embrace the eighteen tones of keyed instruments which all lie in order for use. The power and extent of each are complete in itself, rising and developing, not from any inherent property in matter, but from the life communicated to matter. In the whole process of harmony there are limits, and yet it is illimitable. Its laws compel each key-note to follow certain rules within certain bounds; each separate key-note, being the fountain of its own system, has its own point of rest, and series after series rise and enlarge, or fall and diminish infinitely. [Harmonies of Tones and Colours, Diagram I - The Eighteen Tones of Keyed Instruments, page 22a]

We here trace the twelve harmonies developing in succession. Notice how exactly they all agree in their mode of development; also the use of the chasms between E and F, B and C. Remark also the beautiful results from the working of the double tones, especially C#-D?, and E#-F?, causing the seven tones of each harmony, when ascending, to rise one tone, and, descending, to reverse this movement. F#-G? is the only double tone which acts as F# when a key-tone, and G? when the root of D?. The root of each harmony is the sixth and highest tone in each succeeding harmony, rising one octave; when it is a double tone, it sounds according to the necessity of the harmony. The intermediate tones are here coloured, showing gradual modulation. The isolated fourths (sounding sevenths) were the previously developed key-tones; these also alter when they are double tones, according to the necessity of the harmony. Beginning with B, the isolated fourth in the harmony of C, the tones sound the twelve notes of a keyed instrument, E# being F?, and the double tones, some flats, some sharps. [Harmonies of Tones and Colours, Combinations of dissonance, rests, page 24]

The twelve key-notes, with the six notes of each as they veer round in trinities, are again written in musical clef, and the scales added. The key-note leads the scale, and, after striking the two next highest notes of the seven of the harmony, goes forward, with its four lowest, an octave higher. The seven of each harmony have been traced as the three lowest, thus meeting the three highest in three pairs, the fourth note being isolated. Notwithstanding the curious reversal of the three and four of the scale, the three lowest pair with the three highest, and the fourth with its octave. The four pairs are written at the end of each line, and it will be seen how exactly they all agree in their mode of development. Keys with sharps and keys with flats are all mingled in twelve successive notes. If we strike the twelve scales ascending as they follow each other, each thirteenth note being octave of the first note of the twelve that have developed, and first of the rising series, the seventh time the scales gradually rise into the higher series of seven octaves beyond the power of the instrument. Descending is ascending reversed. After the seven and octave of a scale have been sounded ascending, the ear seems to lead to the descending; but ten notes of any scale may be struck without the necessity of modulation; at the seventh note we find that the eleventh note in the progression of harmonics rises to meet the seventh. For instance, B, the seventh note in the scale of C, must have F#. This point will be fully entered into when examining the meeting of fifths. To trace the scale of C veering round as an example for all, we may begin with C in Diagram II., and go forward with F, G, A, and B an octave higher. If the twelve scales were traced veering round, they would be found to correspond with the twelve as written in musical clef. [Harmonies of Tones and Colours, Diagram IV - The Development of the Twelve Major Scales, page 26a]

ON a keyed instrument only twelve are major key-notes, but as the double tones C#-D? and F#-G? are roots, there are fourteen different chords. The fourteen that are roots are written in musical clef. As an example of the major chords in the different keys, we may examine those in the key of C. A major fifth includes five out of the seven of its key; with the third or central note it is the threefold chord, or fourfold when the octave note is added. Including the silent key-notes, a threefold chord embraces eight, or, counting the double tones, not including E#, eleven. The first and second chords of the seven of the harmony are perfect major chords in the key of C; the central note of the third chord, being #C-?D, is a discord. The first pair of fifths in the scale, with its central note, is a chord of the key; if we include the octave, the last pair of fifths, with its central note, is the same chord an octave higher than the lowest chord of the seven. Of the chords written in musical clef of the twelve keys, the octave chord is only written to C, the seven of each having two chords and the scale one, thirty-six in all, or forty-eight if the octave chords are added. Notice how the chords of each seven and the chord of its scale are altered. [Harmonies of Tones and Colours, Diagram V - The Chords of the Twelve Major Keys, page 27a]

The 12 Key-notes and their trinities and scales written in musical clef, with their chords added, all rising in the two octaves, as before. [Harmonies of Tones and Colours, The 12 Keynotes and Their Trinities and Scales, page 28c]

THE twelve keys have been traced following each other seven times through seven octaves, the keys mingled, the thirteenth note being the octave, and becoming first of each rising twelve. Thus developing, the seven notes of each eighth key were complementary pairs, with the seven notes of each eighth key below, and one series of the twelve keys may be traced, all meeting in succession, not mingled. When the notes not required for each of the twelve thus meeting are kept under, the eighths of the twelve all meet by fifths, and as before, in succession, each key increases by one sharp, the keys with flats following, each decreasing by one flat; after this, the octave of the first C would follow and begin a higher series. It is most interesting to trace the fourths, no longer isolated, but meeting each other, having risen through the progression of the keys to higher harmonies. In the seven of C, B is the isolated fourth, meeting F#, the isolated fourth in the key of G, and so on. Each ascending key-note becomes the root of the fifth key-note higher; thus C becomes the root of G, &c. [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys1, page 29]

The following table shows the regularity of each seven of the twelve key-notes ascending by fifths, and the use of the two poles is again seen. The key-notes and their trinities are closely linked into each other, the three highest notes of the lower fifth key becoming the three lowest of the higher fifth key, and the four lowest becoming the four highest in an octave higher. The twelve keys, rising in each note a tone higher and descending a tone lower, cause the meetings by fifths. Having examined the table, we may strike the keys by fifths as written in the musical clef, beginning with the lowest C in [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys1, page 29]

In the development of the key-notes, the sharp or flat is written to each note, but not to the keys. The reversal of the three and four notes of each seven of the twelve key-notes and their trinities meeting by fifths having been traced, we will now examine the twelve scales meeting by fifths, and the results arising from the reversal of the three and four notes of each fifth lower scale in the fifth higher. Take as an example the scale of C: C D E F G A B, and that of G: G A B C D E F#. The four lowest notes of the seven of C are the four highest, an octave higher, in G; F, the central and isolated note of the seven of C, having risen a tone higher than the octave in the scale of G. The twelve scales thus modulate into each other by fifths, which sound the same harmonies as the key-notes and their trinities. Refer to the twelve scales written in musical clef ascending by fifths, and strike them, beginning at the lowest C in the bass clef; this scale sounds no intermediate tones, but these must be struck as required for all the scales to run on in fifths. After striking the seven notes of C, if we fall back three, and repeat them with the next four notes of the seven; or strike the seven and octave of C, and fall back four, repeating them and striking the next four, the four last notes of each scale will be found to be always in the harmony of the four first of the fifth higher scale. When the twelve scales ascending have been thus gained, as we trace them also on the table, they may be struck descending by following them as written in musical clef upwards, and [Harmonies of Tones and Colours, Diagram VII - The Modulating Gamut of the Twelve Keys2, page 30]

THE term "key" in the minor developments must be taken in the sense in which it is understood by musicians, although it will be seen that it is only the seven of the harmony that are the relative minor keys of the majors, the scales with their chords sounding other keys. The grandeur, combined with simplicity, of the laws which develope musical harmonies are strikingly exhibited in the minor keys. Although at first they appear most paradoxical, and, comparing them with the majors, we may almost say contradictory in their laws of development, when they are in some degree understood, the intricacies disappear, and the twelve keys follow each other (with the thirteenth octave), all exactly agreeing in their mode of development. I shall endeavour to trace them as much as possible in the same manner as the majors, the lowest developments of the minor keys being notes with scales and chords, the notes always sounding their major harmonies in tones. Here an apparently paradoxical question arises. If the major keys are gained by the notes sounding the major tones, how are the minor keys obtained? Strictly speaking, there are no minor key-notes: the development of a minor harmony is but a mode of succession within the octave, caused by each minor key-note employing the sharps or flats of the fourth major key-note higher; and with this essential difference, it will be seen in how many points the developments of major and minor harmonics agree. I have carefully followed the same laws, and if any capable mind examines the results, I am prepared for severe criticism. I can only express that it was impossible to gain any other results than the seven of the harmony, the ascending and the descending scale and the chords combining three different keys. [Harmonies of Tones and Colours, Diagram VIII - On the Development of the Twelve Minor Harmonies, page 32]

THE same laws are followed here as in the development of the major scales. In that of A, F, the sixth note, has risen to F#, in order to meet B, which has previously sounded. In descending, the seventh note, B, falls to B?, in order to meet F, which has also previously sounded. The notes, ascending or descending, always follow the harmony of their key-note, except when rising higher or falling lower to meet in fifths. We may here trace the twelve, the ascending scale sounding the fifth harmony higher than its key-note, and, in descending, sounding the fifth lower harmony. The four pairs of each scale are written at the end of the lines. If we strike the twelve scales as they follow in succession, the thirteenth note being the octave of the first, and leader of a higher twelve; having gained them six times, at the seventh they gradually rise (though beyond the power of a keyed instrument) into the higher series of seven octaves, and again, in descending, they fall lower, and are linked into the lower series of seven octaves. Nine notes of any ascending minor scale may be struck without the necessity of modulating beyond the fifth harmony. For example, in the scale of A, its tenth note, C#, rises to meet the sixth note, which has previously sounded. In descending, E?, the eleventh note, meets B?, the seventh note, which has previously sounded. The scale of A may be traced veering round by reference to Diagram IX., beginning with A, and carrying the four lowest notes an octave higher, F rising to F# in ascending, B falling to B? in descending. [Harmonies of Tones and Colours, Diagram XI - The Twelve Minor Keynotes with the Six Note of Each, page 36a]

ALTHOUGH only twelve notes of a keyed instrument develope perfect minor harmonics, there are fifteen different chords, the double tones D#-E?, E#-F?, A#-B? all sounding as roots. The fifteen roots are written in musical clef. A major and a minor fifth embrace the same number of key-notes, but the division into threefold chords is different. In counting the twelve, a major fifth has four below the third note of its harmony, and three above it; a minor fifth has three below the third note of its harmony, and four above it. A major seventh includes twelve key-notes, a minor seventh only eleven. As an example of the minor chords in the different keys, we may first examine those in the key of A, written in musical clef. The seven of its harmony have two threefold chords, and two of its ascending scale. If we include the octave note, the highest chord of the descending scale is a repetition (sounding an octave higher) of the lowest chord of the seven in its harmony, and the second chord of the descending scale is a repetition of the first chord of its ascending scale. These two repetition chords are only written to the key of A: the chords of the other eleven keys will all be found exactly to agree with those of A in their mode of development. We may again remark on the beautiful effect which would result if the colours of the minor chords could be seen, with the tones, as they develope. [Harmonies of Tones and Colours, Diagram XII - The Chords of the Twelve Minor Keys, page 37a]

[Harmonies of Tones and Colours, Diagram XIII - The Twelve Keynotes with Their Trinities, page 38a]

Let us first examine the meeting of the key-notes and their trinities in musical clef; the isolated fourths rising through the progression of the twelve now meet, seven and seven pairing. We must notice how closely they are linked into each other, the three highest notes of the lower seven being the three lowest of the higher seven an octave higher, and the four lowest becoming the four highest an octave higher; we descend by following the keys as written in musical clef upwards. [Harmonies of Tones and Colours, Diagram XIV - The Modulating Gamut of the Twelve Minor Keys by Fifths1, page 39]

TO recapitulate from the beginning, observe, firstly, the twelve major key-notes as they have developed from within themselves in succession, six tones in trinities seven times through seven octaves, each thirteenth note being the octave of the first note of the twelve that have developed, and being also the first of the higher series. We may retrace all as still sounding their tones, the key-notes leading the ear to the six notes of each harmony, the keys with sharps and those with flats being mingled. The ascending and descending scales always agree in their harmonies with the key-notes and their trinities. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]

Thirdly, the twelve minor keys as they develope in succession seven times through seven octaves, always sounding their major harmony in trinities, and, as with the majors, each thirteenth note being the octave of the first note of the twelve, and first of the following series, the keys all mingled. [Harmonies of Tones and Colours, Diagram XV - The Twelve Major and the Twelve Minor Keys, page 42a]

"I esteem myself fortunate in being introduced to you, and becoming acquainted with your beautiful work on 'Tones and Colours.' I have, to the best of my ability, worked out your idea, by writing down in music the various discords in use amongst musicians, and resolving them according to the laws of Harmony, and I find in all cases the perfect triad agrees with what you term the trinities in colours. The way in which you find the whole circle of Major and Minor keys by pairs in colours is deeply interesting, and must be true. The only point of divergence between your system and that recognised by all musicians is the ascending Minor Scale. No musically trained ear can tolerate the seventh note being a whole tone from the eighth. The Minor second in the lower octave descending is very beautiful, and it is strange how all composers feel a desire to use it. To mention one case out of hundreds, I may cite Rossini's well-known air, 'La Danza.'
"Yours faithfully,
"W. CHALMERS MASTERS." [Harmonies of Tones and Colours, Supplementary Remarks and Diagrams, page 53]

sixth note, which would be Creation perfected, without entering upon the fifth higher key; and it cannot sound the seventh falling into the octave without discord. Therefore the eighth note is not the octave of the first, as it is the fourth note of the fifth higher key. [Harmonies of Tones and Colours, Supplementary Remarks, page 54]

The Major Scales are the type of Creation perfected—man being created, and the Almighty resting—every Major Scale developing the sixth and seventh notes, and the eighth the octave of the first. Therefore, every Major Scale includes the Sabbath, or Rest. [Harmonies of Tones and Colours, Supplementary Remarks, page 54]

The Minor Gamut modulating in the meeting of fifths through seven octaves. We may here trace the twelve, each fifth note becoming the higher key-note. But the sixth and seventh notes of the scale are discords. For example, in the key of A, the sixth note, F?, is a discord with the second note, B?; and the seventh note cannot be sounded as G# falling into the eighth, without being a discord with the third note, C?. No octave can be sounded in the Minor Scale, as it has risen into the fifth higher key of E. [Harmonies of Tones and Colours, The Minor Gamut Modulating in the Meeting of Fifths61, page 65]

---

Vibration Analysis
The Interval between two frequencies with a ratio of 2 to 1. Starting from a given frequency, one octave higher is twice that frequency; one octave lower is half that frequency. (Field of Rotating Machinery Measurement, Monitoring and Analysis)

Alex Petty web site. Shows intervals for 100 octaves.
Alex Petty

---

In music, an octave (Latin: octavus: eighth) or perfect octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". It may be derived from the harmonic series as the interval between the first and second harmonics.

Three commonly cited examples of melodies featuring the perfect octave as their opening interval are "Singin' in the Rain", "Somewhere Over the Rainbow", and "Stranger on the Shore".

The octave has occasionally been referred to as a diapason.

To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. The octave above or below an indicated note is sometimes abbreviated 8va (= Italian all'ottava), 8va bassa (= Italian all'ottava bassa, sometimes also 8vb), or simply 8 for the octave in the direction indicated by placing this mark above or below the staff. Wikipedia, Octave

---

Buckminster Fuller
Synergistics Dictionary: OCTAVE
"Compression is locally expressive in discrete tones and frequencies internal to the octave. Tension is both internal and external to the octave and is harmonic with either the unit octave or octave pluralities." [Buckminster Fuller - Synergetics Dictionary]

See Also

---

1st octave
2nd octave
3rd octave
4th octave
6th octave
7th octave
8th octave
9th octave
B Flat 3rd Octave
C 1st Octave
D 2nd Octave
Diminished
Diminished Eighth
Diminished Octave
diminished seventh
E Sharp 3rd Octave
Eighth
eighth note
Etheric Elements
Figure 1.8 - Electromagnetic Scale in Octaves
Figure 11.01 - Octave composed of Equal Thirds and Triads
Figure 12.11 - Russells Locked Potential Full Ten Octave Gamut
Figure 12.12 - Russells Multiple Octave Waves as Fibonacci Spirals
Figure 12.12 - Russells Multiple Octave Waves as Fibonacci Spirals - See Also
Figure 17.03 - Analysis of the Octave Gravity Bar
Figure 7B.10 - Russells Periodic Chart of the first four octaves of proto-matter
Figure 9.16 - Russells 1-4 Octaves of Matter as Integrated Light - The Universal Constant
Figure 9.17 - Russells Ten Octaves of Matter as Integrated Light - The Universal Constant
genesis of octaves
Interval
Law of Octave
Major Seventh
Minor Seventh
Music
Octave
octave chord
Octave Relationships
Perfect Octave
Proportion
Ramsay - The Great Chord of Chords, the Three-in-One17
Ratio
RULE OF THE OCTAVE
Scale of the Forces in Octaves
seed of the octave wave
Square Law
The Octave Wave - painting
The Russell Nine Octave Chart of the Elements
thirteen
thirteenth note
thirteenth octave
11.15 - Indig Numbers - Inert Gases and Octave Position
12.17 - Note about Octave Relationships in Russells System
12.18 - Multiple Octave Progression