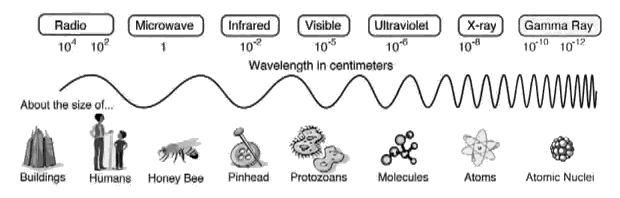
In physics, the wavelength is the spatial period of a periodic wave — the distance over which the wave's shape repeats. It is thus the inverse of the spatial frequency. Wavelength is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. Wavelength is commonly designated by the Greek letter lambda (?). The term wavelength is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.
Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.
Wavelength depends on the medium (for example, vacuum, air, or water) that a wave travels through.
Examples of wave-like phenomena are sound waves, light, water waves and periodic electrical signals in a conductor. A sound wave is a variation in air pressure, while in light and other electromagnetic radiation the strength of the electric and the magnetic field vary. Water waves are variations in the height of a body of water. In a crystal lattice vibration, atomic positions vary.
Wavelength is a measure of the distance between repetitions of a shape feature such as peaks, valleys, or zero-crossings, not a measure of how far any given particle moves. For example, in sinusoidal waves over deep water a particle near the water's surface moves in a circle of the same diameter as the wave height, unrelated to wavelength. The range of wavelengths or frequencies for wave phenomena is called a spectrum. The name originated with the visible light spectrum but now can be applied to the entire electromagnetic spectrum as well as to a sound spectrum or vibration spectrum. Wikipedia, Wavelength
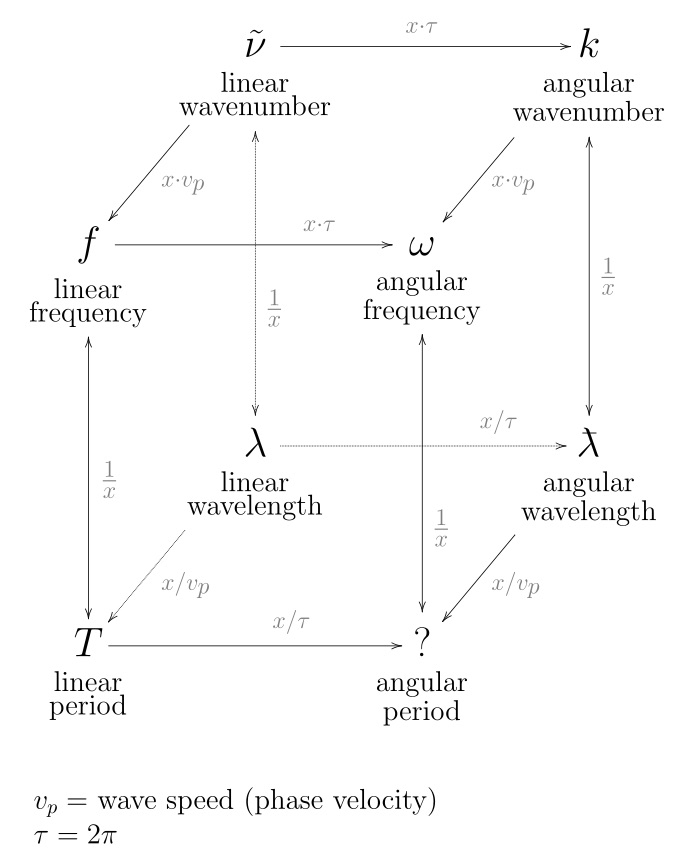
Distance measured along line of propagation, between two points that are in phase on adjacent waves.
[Anderson, Philip C.; The Spectral Energy Value System; Applied Spectroscopy, Vol. 29, #1, 1975.]
To ascertain the wavelength of any given sound - divide the velocity of sound by its vibration number.
The wavelength of any given sound, increases with the temperature.
The temperature remaining constant, the length of the sound wave determines the pitch of the sound produced. [Harris, T. F.; Hand Book of Acoustics, 5th edition; J. Curwen & Sons, London, 1903?]
The range of musical pitch is from about 40 to 4,000 vibrations per second
The length in space of one complete cycle of sound wave.
A = speed of sound/frequency = c/f
where A = wavelength in ft or m.
Wavelength can be calculated from the following equation:
Wavelength (meters) = Velocity 300,000,000 (meters/sec) / Frequency (cycles/sec)
If we substitute 1.5 MHz for the frequency as shown, then
200 meters = 300,000,000 / 1,500,000
[Hirschorn, Martin; Compendium of Noise Engineering - Part I Sound & Vibration Magazine, July 1987.; Sound & Vibration Magazine, July 1987.]
calculate Frequency/Wave Length
Hughes
On colours developing by the same laws as musical harmonies
—The physical properties of light and darkness briefly considered
—If the laws are correctly gained, harmonics of tones and of colours will agree
—Quotation from a lecture by Professor W. F. Barrett on the order of sonorous and luminous wave-lengths
—Fountain of musical harmonics, E root of B; in colours yellow and ultra-violet, being tints and shades of white and black
—All harmonics of sound and colour condense into a primo springing from the fountain
—Multequivalency of tones and colours
—Wünsch's views nearly one hundred years ago
—Clerk Maxwell's, Lord Rayleigh's, and [Harmonies of Tones and Colours, Table of Contents1 - Harmonies]
suspected. Let us take as our standard of colours the series given by the disintegration of white light, the so-called spectrum: as our standard of musical notes, let us take the natural or diatonic scale. We may justly compare the two, for the former embraces all possible gradations of simple colours, and the latter a similar gradation of notes of varying pitch. Further, the succession of colours in the spectrum is perfectly harmonious to the eye. Their invariable order is— red, orange, yellow, green, blue, indigo, and violet; any other arrangement of the colours is less enjoyable. Likewise, the succession of notes in the scale is the most agreeable that can be found. The order is—C, D, E, F, G, A, B; any attempt to ascend or descend the entire scale by another order is disagreeable. The order of colours given in the spectrum is exactly the order of luminous wave-lengths, decreasing from red to violet. The order of notes in the scale is also exactly the order of sonorous wave-lengths, decreasing from C to B." [Harmonies of Tones and Colours, On Colours as Developed by the same Laws as Musical Harmonies2, page 19]
"Comparing wave-lengths of light with wave-lengths of sound—not, of course, their actual lengths, but the ratio of one to the other—the following remarkable correspondence at once comes out:—Assuming the note C to correspond to the colour red, then we find that D exactly corresponds to orange, E to yellow, and F to green. Blue and indigo, being difficult to localise, or even distinguish in the spectrum, they are put together; their mean exactly corresponds to the note G: violet would then correspond to the ratio given by the note A. The colours having now ceased, the ideal position of B and the upper C are calculated from the musical ratio." [Harmonies of Tones and Colours, On Colours as Developed by the same Laws as Musical Harmonies2, page 19]
See Also
Compression Wave
convert frequency to wavelength
Figure 12.10 - Russells Locked Potential Wave
Figure 12.12 - Russells Multiple Octave Waves as Fibonacci Spirals
Figure 13.13 - Gravity Syntropic and Radiative Entropic Waves
Figure 14.07 - Love Principle: Two sympathetic waves expanding from two points have one coincident centering locus
Figure 6.10 - Wave Dynamics between Cube Corners
Figure 6.9 - Russell depicts his waves in two ways
Figure 7.1 - Step 1 - Wave Vortex Crests at Maximum Polarization
Figure 8.1 - Russells Painting of Wave Form Dynamics
Figure 8.10 - Each Phase of a Wave as Discrete Steps
Figure 8.11 - Four Fundamental Phases of a Wave
Figure 8.14 - Some Basic Waveforms and their constituent Aliquot Parts
Figure 8.2 - Compression Wave Phase Illustration
Figure 8.3 - Coiled Spring showing Longitudinal Wave
Figure 8.4 - Transverse Wave
Figure 9.10 - Phases of a Wave as series of Expansions and Contractions
Figure 9.11 - Compression Wave with expanded and contracted Orbits
Figure 9.13 - Wave Flow as function of Periodic Attraction and Dispersion
Figure 9.14 - Wave Flow and Phase as function of Particle Rotation
Figure 9.15 - Wave Flow and Wave Length as function of Particle Oscillatory Rotation
Figure 9.5 - Phases of a Wave as series of Expansions and Contractions
Figure 9.9 - Wave Disturbance from 0 Center to 0 Center
In the Wave lies the Secret of Creation
Longitudinal Wave
Nodal Waves
Rayleigh Wave
Standing Wave
Standing Waves
Table 12.02 - Length Area and Volume Math
Table 12.02.01 - Wavelengths and Frequencies
wave number
12.05 - Three Main Parts of a Wave
12.12 - Length
16.06 - Electric Waves are Sound Waves
3.8 - There are no Waves
3.9 - Nodes Travel Faster Than Waves or Light
8.3 - Conventional View of Wave Motion
8.4 - Wave types and metaphors
8.5 - Wave Motion Observables
8.6 - Wave Form Components
8.8 - Water Wave Model
9.2 - Wave Velocity Propagation Questions
9.30 - Eighteen Attributes of a Wave
9.31 - Oscillatory Motion creating Waveforms
9.34 - Wave Propagation
9.35 - Wave Flow
