On the Intensity or Loudness of Musical Sounds.
We have seen that the pitch of a sound depends solely upon the rapidity with which the vibrations succeed one another. We have next to study the question: "Upon what does the Loudness or Intensity of a sound depend?"
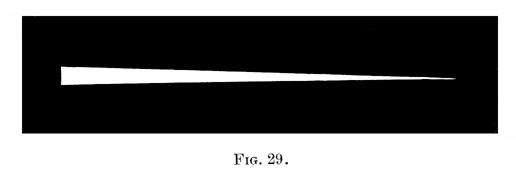
Gently pluck a violin string. Notice the intensity of the resulting sound, and also observe the extent or amplitude of the string's vibration. Pluck it harder; a louder sound is heard, and the string is seen to vibrate through a greater space. Pluck it harder still; a yet louder sound is produced, and the amplitude of the vibrations is still greater. We may conclude, from this experiment, that as long as we keep to the same sounding body, the intensity of the sound it produces, depends upon the amplitude of its vibrations; the greater the amplitude, the louder the sound. This fact may be strinkingly illustrated by the following experiment. Fasten a style of paper, or better still, parchment, to one prong of a large tuning fork. Coat a slip of glass on one side with lamp black, and lay it, with the coated side upwards, on a smooth board, having previously nailed on the latter a straight strip of wood, to serve as a guide in subsequently moving the glass slip. Now strike the fork sharply, and immediately hold it parallel to the glass, in such a way, that the vibrating style just touches the lamp black. Move the glass slip slowly along under the tuning fork. The latter, as it vibrates, will remove the lamp black, and leave a clean wedge-shaped trace on the glass, as seen in fig. 29. As the width of the trace at any point is evidently the amplitude of the vibration of the fork, at the time that point was below it, we see that the amplitude of the vibrations of the fork gradually decreases till the fork comes to rest; and as the sound decreases gradually till the fork becomes silent, we see that the intensity of its sound depends upon the amplitude of its vibrations.
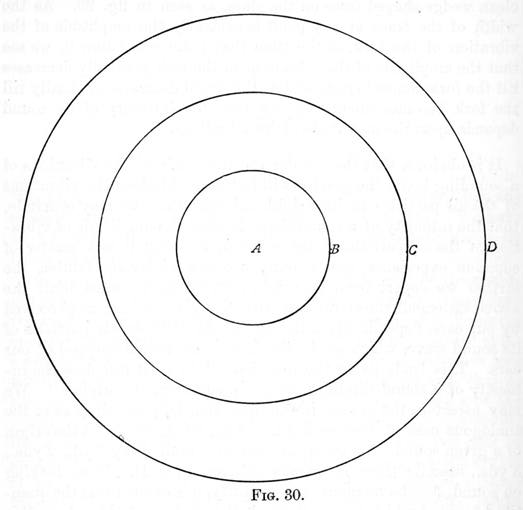
It is obviously, that the greater the amplitude of the vibrations of a sounding body, the greater will be the amplitude of the vibrations of the air particles in its neighbourhood; thus we may conclude, that the intensity of a sound depends upon the amplitude of vibration of the air particles in the sound wave. But it is a matter of common experience, that a sound becomes fainter and fainter, the farther we depart from its origin; therefore, we must limit the above statement thus: the intensity of a given sound, as perceived by our ears, depends upon the amplitude of those air particles of its sound wave, which are in the immediate neighbourhood of our ears. This leads us to the question: "At what rate does the intensity of a sound diminish, as we recede from its origin?" We may ascertain the answer to this question, by proceeding as in the analogous case of heat or light. Thus, let A, fig. 30 be the origin of a given sound. At centre A, and with radii of say 1 yd., 2 yds., 3 yds., describe three imaginary spheres, B, C, D. Now, looking on sound, for the moment, as a quantity, it is evident that the quantity of sound which passes through the surface of the sphere B is identical with the quantity that passes through the surface of the spheres C and D. But the surfaces of spheres vary as the squares of the radii; therefore, as the radi of the spheres B, C, and D are 1, 2, and 3 yds. respectively, their surfaces are as 12 : 22 : 32 that is, the spherical surface C is four times as great, and D 9 times as great, as the spherical surface B. We see, therefore, that the quantity of sound, which passes through the surface of B, is, as it were, spread out fourfold as it passes through C, and ninefold as it passes through D. It follows, therefore, that one square inch of C will only receive 1/4 as much sound as a square inch of B, and one square inch of D only 1/9 as much. Thus, at distances of 1, 2, 3, from a sounding body, the intensities are as 1, 1/4, and 1/9; that is, as we recede from a sounding body, the intensity diminishes in proportion to the square of our distance from the body, or more concisely, "The intensity of a sound varies inversely as the square of the distance from its originâ€. See Square Law, Inverse Square Law
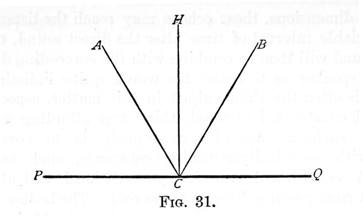
It should be clearly, noted, however, that the conditions under which the above "law of inverse squares," as it is called, is true, rarely or never obtain. The chief disturbing elements in the application of this law are echoes. When a ray of light strikes any reflecting surface at right angles, it is reflected back in the direction whence it came. If a ray of light, A C, fig. 31, does not fall at right angles upon a reflecting surface P Q, it is reflected along a line C B, which is so situated, that the angle B C H is equal to the angle A C H; H C being at right angles to P Q. Just so with sound. A person standing at B would hear a sound from A, first as it reaches him in the direction A B, and directly after, along the line C B. If the distances A B and A C B were each only a few yards, the two sounds would be indistinguishable, but if there were any considerable difference between these two distances, the two sounds would be separately heard, the latter being termed the echo of the former. Therefore, when a vibrating body emits a sound in any room or hall, the waves which proceed from it in all directions, strike the walls, floor, ceiling, and also the reflecting surfaces of the various objects in the place, and are reflected again and again from them. Thus the direct and reflected sounds coalesce, and interfere with one another, in the most complicated manner, and the simple law of inverse squares is no longer applicable. This is still the case, even in the open air, away from all surrounding objects, for the ground will here present a reflecting surface, and other invisible reflectors are found, as Professor Tyndall has shown, in the surfaces which separate bodies of air of different hygrometric [density] states and of different temperatures. See Principle of Regeneration
This may be put in another way. It is a condition of the truth of the law of inverse squares, as above shown, that the sound shall be able to spread outwards in all directions; if this is not the case, the law no longer holds good. Now, in a building, this is not the case; the sound is prevented from spreading by the roof, floor, and walls. If the sound can be entirely prevented from spreading, its intensity will not diminish at all. This is the principle of the speaking tube. In this instrument, the vibrations of the air particles are transmitted undiminished, except by friction against the side of the tube, and by that part of the motion which is given up to the substance of the tube itself; thus sound can be transmitted to great distances in such tubes. Regnault, experimenting with the sewer conduits of Paris, found that the report of a pistol was audible through them, for a distance of 6 miles.
The bad acoustical properties of a building are generally due to echoes. A sound from the lips of a speaker, in a building, reaches the ear of the listener directly, and also after one or more reflections from the ceiling, walls, floor, and so on. If the building be of considerable dimensions, these echoes may reach the listener's ear at an appreciable interval of time after the direct sound, or after one another, and will then so combine with the succeeding direct sound from the speaker as to make his words quite indistinguishable. The roof is often the chief culprit in this matter, especially when lofty, and constructed of wood, this latter affording an excellent reflecting surface. An obvious remedy is to cover such a surface with some badly-reflecting substance, such as a textile fabric. A sound-board over the speaker's head, will also prevent the sound from passing directly to the roof. The bodies and clothes of the persons forming an audience, are also valuable in preventing echoes. Professor Tyndall, to whose work on sound the student is referred for further information on this subject, says that, having to deliver a lecture in a certain hall, he tried its acoustical properties beforehand, and was startled to find that when he spoke from the platform, a friend he had with him, seated in the body of the empty hall, could not distinguish a word, in consequence of the echoes. Subsequently, when the hall was filled with people, the Professor had no difficulty in making himself distinctly heard in every part. Again, everyone must have noticed the difference between speaking in an empty and uncarpeted room, in which the echoes reinforce the direct sound, and speaking in the same room carpeted, and furnished, the echoes in this case being deadened by the carpets, curtains, &c.
Summary.
The Intensity of the sound produced by a vibratory body, depends upon the amplitude of its vibrations.
The Intensity of a sound varies inversely as the square of the distance from its origin, only when the sound waves can radiate freely in all directions without interruption.
Sound is reflected from elastic surfaces in the same way as light, thereby producing echoes.
Sound is well reflected from such surfaces as wood, iron, stone, &c., while cloths, carpets, curtains, and textile fabrics in general, scarcely reflect at all.
