"This intricate and extremely complex idea cannot be more than touched upon here but the simplicity of its fundamental basis is so plainly written in Nature that its complexities cannot elude one who understands the universal plan. To put it briefly Nature is aiming at the true sphere in all her gyroscopic turnings. She finishes her sphere only in one part of the universal machine which is half way around the cycle where the wheels are the same size. In the wave this position is at trough and crest. At this position an element called carbon crystallizes in true cube. It is the only element which does crystallize in absolutely symmetrical true cube because it is the pivotal point of ten efforts of Nature to get her two halves equally divided to equal opposites. These ten waves are what are known as the octaves of the elements. The octaves are spiral waves along which the elements are strung like discs on a string. As a matter of fact, the elements are the wheels of the universal machine and the reason for this variance in form, eccentricities, gearing and crystallization is because they all are parts of a sphere within which all separate parts fit together." [Russell, Genero-Radiative Concept]
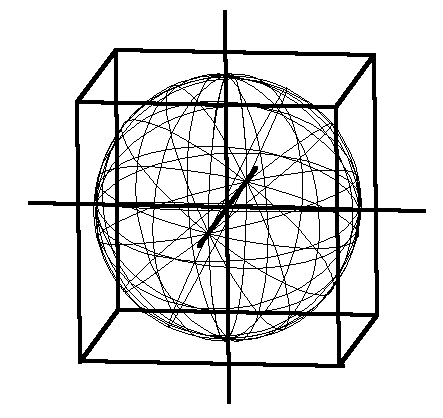
Figure 6.18 - Sphere Circumscribed by Cube (click to enlarge)
Thickness (Volume, Cubic)
Volume increases with decreased potential.
Cube Root of the Volume = SqRt of the Area = Length
"Cubing the Sphere"
(Sphere contiguous with and enclosed by a Cube)
Sphere Volume = 2 X 315 X 5153 = 147,879,835,542
Cube Volume = 65613 = 282,429,536,481
Ratio: 282,429,536,481:147,879,835,542::19,683:10,306 = Diminished Octave (Seventh)
Sphere to Cube = Minor Seventh = 5:9::(2 X 315 X 5153):(65613)(NOTE: Compute music ratios for 3 inner cubes and spheres)
See Also
Cube
Cube Sphere
Cube-Sphere
Cubing the Sphere
Figure 6.17 - Areas and Volumes - Relations and Proportions
Figure 12.09 - Dimensions and Relationships
Quadrature of the Circle
Reciprocating Proportionality
Sphere
Table 12.02 - Length Area and Volume Math
The Universal One, page 163
Volumetric Resonator
See Also
Clocks Wheelwork of Nature 4.4 - Idle Wheels on Natures Machinery
