Sympathetic Vibratory Physics

WaveFunction		WaveFunction
Sympsionics Symbol

(click to enlarge)

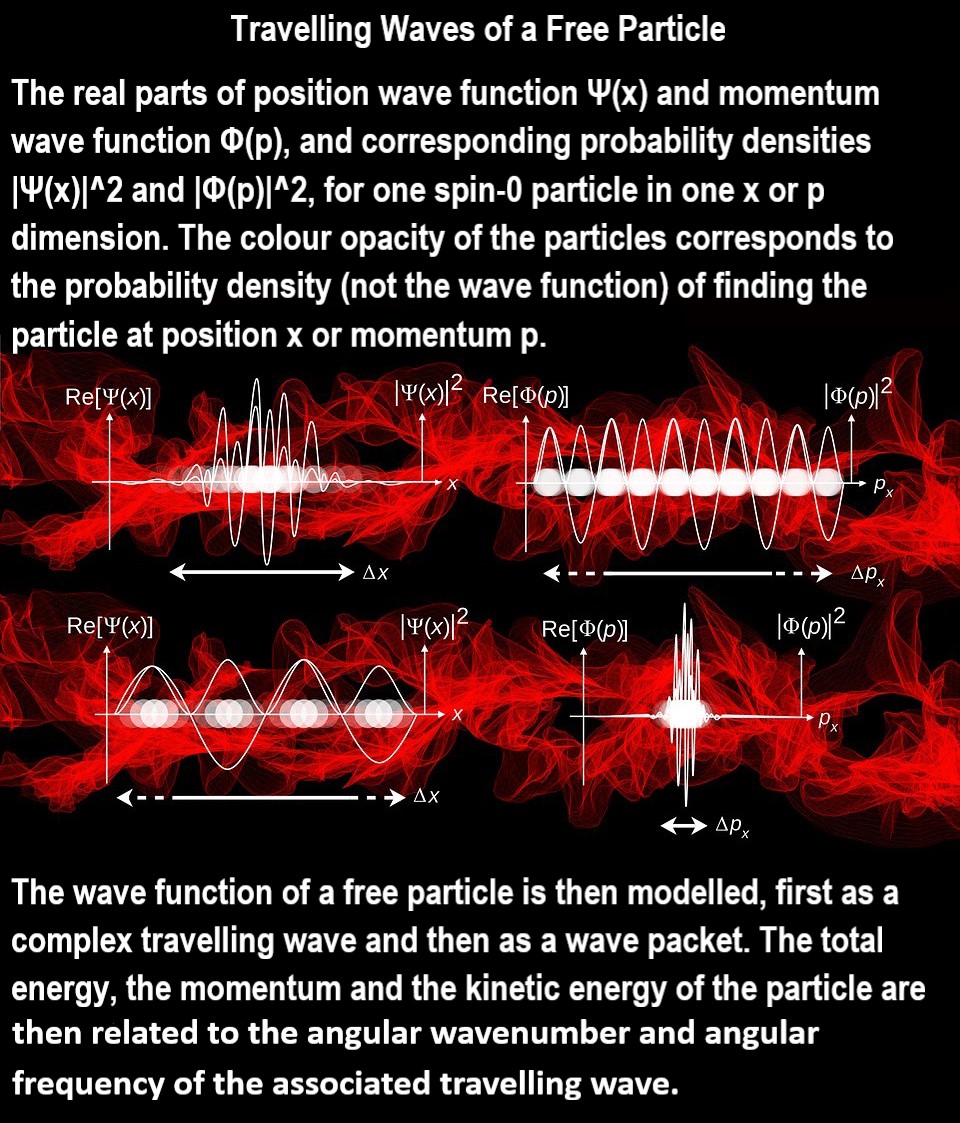
A wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle or system of particles. Typically, it is a function of space or momentum or rotation and possibly of time that returns the probability amplitude of a position or momentum for a subatomic particle. Mathematically, it is a function from a space that maps the possible states of the system into the complex numbers. The laws of quantum mechanics (the SchrÃ¶dinger equation) describe how the wave function evolves over time.

The electron probability density for the first few hydrogen atom electron orbitals shown as cross-sections. These orbitals form an orthonormal basis for the wave function of the electron. Different orbitals are depicted with different scale.

The common application is as a property of particles relating to their wave-particle duality, where it is denoted Ïˆ(position,time) and where | Ïˆ | 2 is equal to the chance of finding the subject at a certain time and position. For example, in an atom with a single electron, such as hydrogen or ionized helium, the wave function of the electron provides a complete description of how the electron behaves. It can be decomposed into a series of atomic orbitals which form a basis for the possible wave functions. For atoms with more than one electron (or any system with multiple particles), the underlying space is the possible configurations of all the electrons and the wave function describes the probabilities of those configurations.

A simple wave function is that for a particle in a box. Another simple example is a free particle (or a particle in a large box), whose wave function is a sinusoid where, in the spirit of the uncertainty principle, the momentum is known but the position is not known.

The modern usage of the term wave function refers to a complex vector or function, i.e. an element in a complex Hilbert space. Typically, a wave function is either:

a complex vector with finitely many components,
a complex vector with infinitely many components,
a complex function of one or more real variables (a continuously indexed complex vector).

In all cases, the wave function provides a complete description of the associated physical system. An element of a vector space can be expressed in different bases; and so the same applies to wave functions. The components of a wave function describing the same physical state take different complex values depending on the basis being used; however the wave function itself is not dependent on the basis chosen. In this respect they are like spatial vectors in ordinary space because choosing a new set of cartesian axes by rotation of the coordinate frame does not alter the vector itself, only the representation of the vector with respect to the coordinate frame. A basis in quantum mechanics is analogous to the coordinate frame in that choosing a new basis does not alter the wavefunction, only its representation, which is expressed as the values of the components above. (underline added)

Because the probabilities that the system is in each possible state should add up to 1, the norm of the wave function must be 1. wikipedia - wavefunction

Sympathetic Vibratory Physics

Bridging Science and Spirituality

Search

wavefunction