Sympathetic Vibratory Physics

courtesy - truthreloaded

This article below appeared in the Winter 2000 Edition of the

University of Science and Philosophy's quarterly magazine,

The Cosmic Light

The Theory of a Musical Universe

"The universe consists solely of waves of motion." relates Walter Russell in chapter 31 of [A New Concept of the Universe]. Another way of saying this is: "There exists nothing other than vibration / oscillation." In Russell's statement lies the base for his next blast at orthodoxy's misbelief in a billiard-ball-like material universe: "Any theory which cannot find a fitting place within the wave has no other place for it in Nature." Hard words for sure but can they stand up to scrutiny? Is it possible to create a paradigm of nature that is structured entirely on wave or vibration theory? Investigating the pioneer work of John W. Keely's Sympathetic Vibratory Physics would lead us to believe this is so.

Logically speaking for such a paradigm to exist it would be couched entirely in vibration or wave terms and concepts and would evolve from the simple to the complex addressing quanta/atomic phenomena all the way through human activity. This author believes this can be done as we are so doing. Inasmuch as a premise voiced ought to be demonstrated it will herein be shown how all vibration is intimately connected (sympathetically) to all other vibration thereby demonstrating 1) the interconnectedness of all things and energies; 2) all things are themselves built up from simple vibration to complex chords using universal Principles of vibration alone; 3) there is no such thing as chaos in the universe; 4) all things exist by virtue of Harmony among the vibrations that make it what it is; and 5) all things are intimately connected by sympathetic vibration.

Some of the information presented here was first published in 1991 (but written earlier) and again in the author's book in 1994, [The Universal Laws Revealed: Keely's Secrets]. This material represents the beginning of the science side of the "science and philosophy" equation. The universe vibrates from end to end as does everything in it. Therefore if we are to investigate and understand this awesome spectacle we are obliged to investigate the nature of vibration or the wave as Russell called it.

If the universe were chaos there would be no Harmony but only degrees of chaos. All sound and vibration would be just plain noise. Noise, therefore is unorganized vibration. But none can doubt there is order recognizable throughout nature from the uniformity of atomic structures and behaviors to spiral galaxies whose swirling arms of orderly stars span light years and billions of years of activity. This innate order inherent in vibratory/oscillatory phenomena has been long recognized, researched and categorized and may be found in at least in part in music theory. In vibratory terms disorderly vibration can be organized in terms of music Principles. Therefore music is organized vibration or sound set in orderly Principles of structure and behavior. The Principles that make sound into harmonious music are the same Principles that govern all associating vibrations throughout the universe - and that includes everything that there is. It will be shown how any given vibration gives rise to a complex yet simple series of subordinate vibrations known generally as harmonics or overtones and these harmonics are arithmetically relative to one another as are musical intervals.

It is generally recognized that everything is a result of vibration and each thing has its own chord of vibration, spectra or vibration signature. This state of vibratory condition is characterized in John Keely's Law of Corporeal Vibrations:

"All coherent aggregates when isolated from like bodies, or when immersed or confined in media composed of matter in a different state, vibrate at a given ascertainable pitch." [John Worrell Keely]

It is a well known and accepted fact that any vibration as in a sound tone will give rise to its octave harmonics. These are the harmonics generally acknowledged by science as multiples of 2, which multiplication derives superharmonics, and divisions by 2 derive subharmonics. These types of harmonic products or results of 2 are called octave harmonics or the overtone series. What is not so generally acknowledged but nevertheless just as true is a tone will give rise to harmonics not divisible 2 but divisible by other numbers such as 3, 5, 7, etc. These other harmonics are developed from and within the octave harmonic series first mentioned, by the octave harmonics interacting arithmetically with and among themselves and with the fundamental. These spontaneously and naturally occurring tones will add and subtract from each other in a perfectly orderly manner giving rise to summation and difference tones sometimes referred to as secondary, tertiary or higher harmonics. When these summation tones are very powerful they are referred to as beat tones or beat frequencies and are considered inharmonic. These arithmetically derived harmonics are characterized in Keely's Law of Cycles and graphically shown in Figure 1.7:

From One (on left) comes all diversity (right) as described by Keely's Law of Cycles.

Figure 1.7 - From One (on left) comes all diversity (at right) as described by Keely's Law of Cycles.

From Harmony (on left) comes all Discord (at right) as described by Keely's Law of Cycles.

(click to enlarge)

See Also

"Coherent aggregates harmonically united constitute centers of vibration bearing relation to the fundamental pitch not multiples of the harmonic pitch, and the production of secondary unions between themselves generate pitches that are discords, either in their unisons, or overtones with the original pitch; from Harmony is generated discord, the inevitable cause of perpetual transformation." [John Worrell Keely]

Vibrations are harmonious to one another when their aliquot parts (factors and/or products) are the same. When these harmonics form unisons or direct harmonic relations the two vibrating aggregates and their chords of vibration are said to be sympathetic to each other; i.e., there is an affinity between them. This unison of frequency (sympathy) dictates that what happens to one vibratorily happens to the other simultaneously. Quantum Mechanics now calls this interaction (when on the quantum level) quantum entanglement. In this case the vibrations of each aggregate or chord and the vibrations active between each are forming unisons or coincident harmonics and are therefore called sympathetic vibrations or sympathetic oscillations and are mutually attractive. Vibrations are considered inharmonic when their aliquot parts or factors are not similar and are mutually repulsive. Most vibrations will have similar factors and/or products and a few dissimilar factors and/or products thereby giving rise to varying degrees of Harmony or dissonance whichever the case may be.

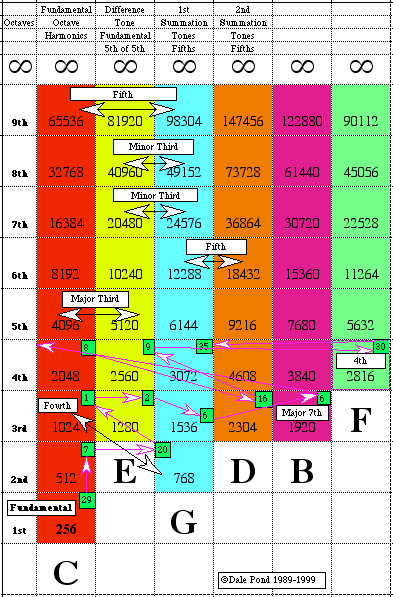
Naturally Ocurring Overtones as Musical Intervals

Figure 1.12 - Naturally Occurring Frequencies Modes and Music Interval Relations

(click to enlarge)

Naturally Occurring Harmonics and Partials

In Figure 1.12 we can see how this process works. Any harmonic series or scale has a base frequency from which all its harmonics are derived. This base tone is called its fundamental or keynote. In the chart a subharmonic of the musical note "C" is used as the fundamental or foundation upon which are self-generated a series of harmonics. This note has a frequency or rate of vibration of 256 cycles per second (cps) or a sub-octave harmonic of middle "C". The smaller squares contain a number representing the relative amplitude or power of this note compared to the other notes soon to be introduced. As a natural process of creative and evolutionary force this fundamental tone will vibrate and this vibration will divide itself into its own superharmonic of 512 cps (2 X 256) which will in turn divide again and again like this ad infinitum according to natural law. Concurrently the number will also resonate and be sympathetic with subharmonics of 128, 64, etc. This process of dividing into smaller and smaller wavelengths is creative and evolutionary and according to Keely's Law of Harmonic Vibrations:

"All coherent aggregates are perpetually vibrating at a period-frequency corresponding to some harmonic ratio of the fundamental pitch of the vibrating body; this pitch is a multiple of the pitch of the atomole (a quantum unit)." [John Worrell Keely]

This new frequency of vibration is the octave harmonic of the fundamental (2 X 1) and is shown placed in the 2nd octave row directly above the first "C1" vibrating on the 1st octave row. The same process continues to unfold for virtually uncountable octaves creating higher and higher frequencies in ever more rising octaves. We will refer to this second "C" as "C2" and so forth for each octave. So far so good, we have a harmonic series born from the lone "C" stretching nearly into infinity both above the progenitor as superharmonics and below it as subharmonics. So in the beginning there was One.... C1 is the creator of C2 which is the created and so forth. This harmonic family of "Cs" are all related by number and this relationship of number can be discovered by factoring and multiplying.

256 factors into:

1x2x2x2x2x2x2x2x2. With this it can be seen the "C" family "gene" (factors) is constructed of a 1 and eight 2s or reduced to simply 1 and 2.

The number 1 will be seen to be shared by all other numbers since all numbers contain 1. One is the ultimate Progenitor having its essence in every thing that was created from it. Therefore One permeates all vibrations equally everywhere and is sympathetic to them all equally because 1:1 is unison, pure Harmony (the superconductive or neutral state).

Vibrations as applied to vibrations are dynamic things not unlike living things. They are creative and evolutionary simultaneously. They are active and prolific in their dynamics as are their harmonic offspring. These discrete tones of the harmonics interact with each other as they intermingle. Being primarily number oriented they will, in a very natural way mix, merge and divide among themselves just like living cells as detailed in the Law of Cycles already mentioned, the Fibonacci Series or Golden Mean and according to Keely's Law of Harmonic Pitch :

"Any aggregate in a state of vibration develops in addition to its fundamental pitch a series of vibration in symmetrical sub-multiple portions of itself, bearing ratios of one, two, three, or more times its fundamental pitch." [John Worrell Keely]

C1 will add its numerical value to C2 and create a third number: 768 cps, which in terms of "Cness" means little. But in relative terms it can be seen the 768 is 3 times the original C1 of 256 cps while 512 cps is 2 times the Creator pitch. These terms of degrees of relativity are then 3 is to 2 as 768 is to 512 . The 3:2 (768:512 reduced to their least common denominators) ratio is a musical ratio of a Perfect Fifth. In this first ratio of spontaneously created harmonics we can see how a base tone gives rise to a naturally occurring harmonic that is identical to two musical notes representing a perfect musical interval of a Perfect Fifth.

768 factors into:

1x2x2x2x2x2x2x2x2x3. The "G" family "gene" is constructed of a 1, eight 2s and a 3. Reduced down we see a Fibonacci connection to the "C" family being 1 + 2 = 3 thus deriving all three "genes" or originating substance of the family. The Fibonacci series was developed as a result of analysis of the reproduction rate of rabbits or as living things. And in these musical notes we see the same genre of self-replicating activity playing throughout the universe. See Locked Potentials for insight into functional properties of Fibonacci Series.

The next harmonic to be born of the intermingling of the lower tones is the rate of 1280 resulting from the additive summation of 512 cps to 768 cps. As an additional impetus to life 1280 is also given more life force by adding in the energy of the 1st harmonic of G being 1536 - C1 = 1280. This naturally derived rate of vibration is equivalent to the musical note "E". E is a musical Major Third above the patriarchal family of C and a Minor Third below the matriarchal family of G.

Interestingly these three first notes derived from a fundamental form the Great Triadic Chord of C, E and G long considered as the most harmonious of all chords. This chord is formed of musical Minor and Major thirds combining to form a Perfect Fifth. This author believes this natural process is revealed allegorically in the first few chapters of Genesis demonstrating the seven intervals of creation resulting from Divine Voice (sound) and Light then evolutionary steps forming the material existence of Adam (C) and Eve (G), i.e., man (Yang) and woman (Yin). In other words, Genesis is an ancient and enlightened scribe's attempt at detailing and conveying what they perceived as this creationist and evolutionary process of life becoming and being what it is - a rhythmic vibratory dance, oscillating and undulating motions governed by the rules of music development. Please notice the intimate connection of threes to nature as regarded by both Russell and Keely:

"The secret of man's ability to control his universe lies in the knowledge of the tonal octave wave and its field. Therefore know the wave in all of its simplicity of three times three in numbered effect, multiplied to infinite complexity but still not passing beyond the three times three of man's easy comprehension." [Walter Russell, A New Concept of the Universe, page 56.]

"Rotation arises through the harmonic interactions of the dominant and enharmonic modes of vibration, in the ratio of 3:9." John Keely, [The Snell Manuscript]

E's "gene pool" is again different from its progenitors:

1280 factors into: 1x2x2x2x2x2x2x2x2x2x5. This "gene pool" reduces to 1, 2 and 5 wherein we can see the harmonious connection to the C and G families in the 1 and 2 being common "genes" or factors of multiplicity which establish a degree of sympathy or Harmony between tones. And the Fibonacci aspect is seen again: 1 + 2 = 3 and 2 + 3 = 5.

Next in line of procreation is "D" having 2304 cps. The "D" family of harmonics are created from a merging of G1 + G2 = 2304 and C3 + E1 = 2304 . D is therefore offspring of several combinations of progenitor tones and has relatively high power of 16.

2304 factors into:

1x2x2x2x2x2x2x2x2x3x3. D's gene pool reduces to 1, 2 and 3 same as the G family just a musical and harmonic Fifth away. While E is a musical third from its parents C and G while D is only a musical Second away. A third in musical terms is considered more harmonious a relationship than a Second which is considered somewhat discordant. The reason for this is the closeness of the numbers. The ratio of numbers in a Second may be so close that when they subtract from one another there arises a slight difference which can become a beat tone and it is this difference (and subsequent beat) that gives rise to the perceived "harshness" of sound of a chord made of these two tones when played together. This new beat tone may have a factor set of numbers not wholely similar to its progenitors. One could liken this "marriage" of Second tones to an inter-familial one wherein offspring may be "aberrant" in formation and or activity. When sounded sequentially one after the other there is a degree of Harmony but together they do not make harmonious music due to the enharmonic character of the beat tone and numbers.

Another interesting harmonic born of this process of evolution of harmonies is an interval close to the note F. An arithmetically derived Perfect Fourth (3:4) above C4 (2048) would yield F at 2730.6 which would be enharmonic. However a naturally occurring summation tone of C4 (2048) + G1 (768) yields 2816 (F) which coincides with a musical Perfect Fourth derived from C4 (2112) when A=440. What this shows is the "pedigree" of a number determines how its harmonics will interface with itself being then harmonious or discordant to some degree. By simply shifting the fundamental by a digit or two changes the degree of concordance. This area of music and Harmony and conversion from naturally occurring harmonics to artificially derived musical intervals(7) is further discussed in Part 11 - SVP Music Model. The author wishes to simply present the idea that all sounds or vibrations when considered as a fundamental will yield a complex series of octave and non-octave harmonics following the rules that govern music development which are in reality an attempt to mirror naturally occurring activities among vibrations. This going from One to Many is the process Russell describes as the formation of the diversity and complexity of matter from the One Idea of Divine Mind. There is a mirror reverse process too and this process is covered elsewhere as for instance in bottom half of Figure 1.5.

There is another kind of additive and substractive synthesis going on in vibrations as they interact. This summation or difference is also in the POWER of the vibrations. Throwing a pebble in a calm pool of water will give rise to concentric rings of waves expanding outward. The rings of waves possess two basic wave characteristics. Each ring is composed of a raised portion of water and a sequential portion of lowered water each portion being above and below the normal level of the water respectively. If another pebble is thrown into the water a second series of concentric rings will arise. The two series of rings will interact. Where the crest of a wave meets another crest of a wave from the other ring series the two crests will add their height to each other thereby creating a momentary increase in height above the unadded portion of each wave. And where a trough meets a trough the reverse will be true. In sound waves this adding and subtracting will occur with harmonics and harmonics of harmonics resulting in quite complex wave configurations. Thus power may be added or subtracted to power just as frequency may be added or subtracted to frequency - all occurring naturally of course. In this process we can see one form of "free energy" developed by the adding together the power of different harmonics.

The Proof

All good theories require a proof before they can be accepted. In our case of musical octave and nonoctave harmonics arising from all vibrations we can present a model.

In November 1989 Sound & Vibration[6] magazine published an interesting article on Chladni wave plate modes and frequencies. The latest technology was used to record and tabulate this intriguing phenomenon. The aim was to find the various naturally occurring frequencies and modes of a vibrating square plate when forced to vibrate thus revealing its natural frequencies or modes of resonance.

In finding the interrelationships of the vibratory activities along the lines of our theory a table of these naturally occurring frequencies and modes was prepared, see chart #2. Common music note intervals are compared along with the various modes and frequencies discovered. It is very interesting to see that the naturally occurring frequencies when compared one to another, as is done with musical pitches to derive intervals, all fall very close to known musical intervals!

Ratio : Ratio	INTERVAL	DECIMAL	DIFFERENCE
		EQUIVALENT
Mode 3 : Mode 2
1472 : 1207 cps		1.219...	actual
6 : 5	Minor Third	1.2	.019
5 : 4	Major Third	1.25	.031
Mode 4 : Mode 3
2105 : 1472 cps		1.430...	actual
64 : 45	Diminished 5th	1.4222	.0078
36 : 25	Diminished 5th	1.44	.01
Mode 2 : Mode 1
1207 : 817 cps		1.477...	actual
36 : 25	Diminished 5th	1.44	.037
3 : 2	Perfect 5th	1.5	.023
Mode 4 : Mode 2
2105 : 1207 cps		1.743...	actual
125 : 71	Augmented 6th	1.736...	.007
7 : 4	Harmonic 7th	1.75	.007
Mode 3 : Mode 1
1472 : 817 cps		1.801...	actual
9 : 5	Tonic 7th	1.8	.001
15 : 8	Major 7th	1.875	.074
Mode 4 : Mode 1
2105 : 817 cps		2.576...	actual
5 : 2	Major 10th	2.5	.076
8 : 3	Perfect 11th	2.666...	.09
	©copyright Dale Pond, 1990-2010

Table of Plate Harmonics and Intervals

Bridging Science and Spirituality

Search

1.21 - It Really Is a Musical Universe