In mathematics, a continuous function (continuity) is a function for which, intuitively, small changes in the input result in small changes in the output. Otherwise, a function is said to be "discontinuous." A continuous function with a continuous inverse function is called "bicontinuous."
Continuity of functions is one of the core concepts of topology, which is treated in full generality below. The introductory portion of this article focuses on the special case where the inputs and outputs of functions are real numbers. In addition, this article discusses the definition for the more general case of functions between two metric spaces. In order theory, especially in domain theory, one considers a notion of continuity known as Scott continuity. Other forms of continuity do exist but they are not discussed in this article.
As an example, consider the function h(t), which describes the height of a growing flower at time t. This function is continuous. In fact, a dictum of classical physics states that in nature everything is continuous. By contrast, if M(t) denotes the amount of money in a bank account at time t, then the function jumps whenever money is deposited or withdrawn, so the function M(t) is discontinuous. (However, if one assumes a discrete set as the domain of function M, for instance the set of points of time at 4:00 PM on business days, then M becomes continuous function, as every function whose domain is a discrete subset of reals is.) Wikipedia - Continuity or Continuous Function
Keely
Every mass is an aggregation of molecules each having its "neutral center" wherein are equated its component forces consisting of the three fundamental modes of vibration. The balanced activity of these vibrations at the "neutral center" without diminution of force, makes possible the permanence of form and matter.
Since the continuity of existence of all molecules and all masses depends on the three fundamental component modes of vibration being held in balance at the "neutral center" it follows that certain orders of vibration can, by their influence on this neutral center, break the balanced equation, divide the components of the molecules, and therefore divide the components of the mass. [PERMANENCE OF FORM AND MATTER]
When Keely's discovery has been made known to scientists, a new field of research will be opened up in the realm of Philosophy, where all eternal, physical, and metaphysical truths are correlated; for Philosophy has been well defined by Willcox as the science of that human thought which contains all human knowledges. He who possesses the structure of philosophic wisdom built up of all knowledges - grand and sublime - has a mental abode wherein to dwell which other men have not. Dr. Macvicar says:- "The nearer we ascend to the fountain-head of being and of action, the more magical must everything inevitably become, for that fountain-head is pure volition. And pure volition, as a cause, is precisely what is meant by magic; for by magic is merely meant a mode of producing a phenomenon without mechanical appliances - that is, without that seeming continuity of resisting parts and that leverage which satisfy our muscular sense and our imagination, and bring the phenomenon into the category of what we call 'the natural' - that is, the sphere of the elastic, the gravitating, the sphere into which the vis inertiae is alone admitted." In Keely's philosophy, as in Dr. Macvicar's "Sketch of a Philosophy," the economy of creation is not regarded as a theory of development all in one direction, which is the popular supposition, but as a cycle in which, after development and as its fruit, the last term gives again the first. Herein is found the link by which the law of continuity is maintained throughout, and the cycle of things is made to be complete: - the link which is missing in the popular science of the day, with this very serious consequence, that, to keep the break out of sight, the entire doctrine of spirit and the spiritual world is ignored or denied altogether." [The Fountain Head of Force]
Russell
"In this Universe, the octaves of the elements of matter "Grow" from seed, just as all things grow from seed. Elements are not fixed created things. They are pressure conditions of light waves. The inert gases are the cosmic seeds of matter in this Universe. They surround the zero from which motion springs and to which it returns. They are the seeds of the octaves of matter, and each octave has a different seed just as different trees has different seeds. The inert gases are the recorders in cosmic seed of this creating universe of infinite continuity." [Russell]
Ramsay
CONTINUITY. - Unbroken sequence. [Scientific Basis and Build of Music, page 25]
"Of these three chords, which constitute a scale or key, Nature next proceeds to generate, in a similar way, a family of scales or keys, and these in two lines, the Major and the Minor. The twice twelve-fold family of keys is brought forth in much the same way as were the chords which constitute them, and as were the notes which constitute the chords. There is a beautiful growth-like continuity in the production of all." [Scientific Basis and Build of Music, page 20]
"As vibrating motions of whatever kind, and however rapid, are made in time, so they all partake of its continuity. Where the one vibration ends the other begins, at an indivisible instant when the string is crossing the right line. An indivisible point is the common limit of the two vibrations; thus they are under the law of continuity.
The contraction and expansion of the air in one vibration is effected in successive times; but the compression of the air of one vibration and the expansion of the air of the preceding one are simultaneous, so they" [Scientific Basis and Build of Music, page 23]
When the major scale has been generated, with its three chords, the subdominant, tonic, and dominant, by the primary mathematical ratios, it consists of forms and orders which in themselves are adapted to give outgrowth to other forms and orders by the law of duality and other laws. All the elements, orders, combinations, and progressions in music are the products of natural laws. The law of Ratio gives quantities, form, and organic structure. The law of Duality gives symmetry, producing the minor mode in response to the major in all that belongs to it. The laws of Permutations and Combinations give orders and rhythms to the elements. The law of Affinity gives continuity; continuity gives unity; and unity gives the sweetness of harmony. The law of Position gives the notes and chords their specific levities and gravities; and these two tendencies, the one upward and the other downward, constitute the vital principle of music. This is the spiritual constitution of music which the Peter Bell mathematicians have failed to discern: [Scientific Basis and Build of Music, page 37]
In the progression - that is, the going on from one to another - of these triplets in harmonizing the octave scale ascending, Nature goes on normally till we come to the passage from the sixth to the seventh note of the scale, whose two chords have no note in common, and a new step has to be taken to link them together. And here the true way is to follow the method of Nature in the birthplace of chords.1 The root of the subdominant chord, to which the sixth of the octave scale belongs, which then becomes a 4-note chord, and is called the dominant seventh; F, the root of the subdominant F, A, C, is added to G, B, D, the notes of the dominant, which then becomes G, B, D, F; the two chords have now a note in common, and can pass on to the end of the octave scale normally. In going down the octave scale with harmony, the passage from the seventh to the sixth, where this break exists, meets us at the very second step; but following Nature's method again, the top of the dominant goes over to the root of the subdominant, and F, A, C, which has no note in common with G, B, D, becomes D, F, A, C, and is called the subdominant sixth; and continuity being thus established, the harmony then passes on normally to the bottom of the scale, every successive chord being linked to the preceding note by a note in common. [Scientific Basis and Build of Music, page 49]
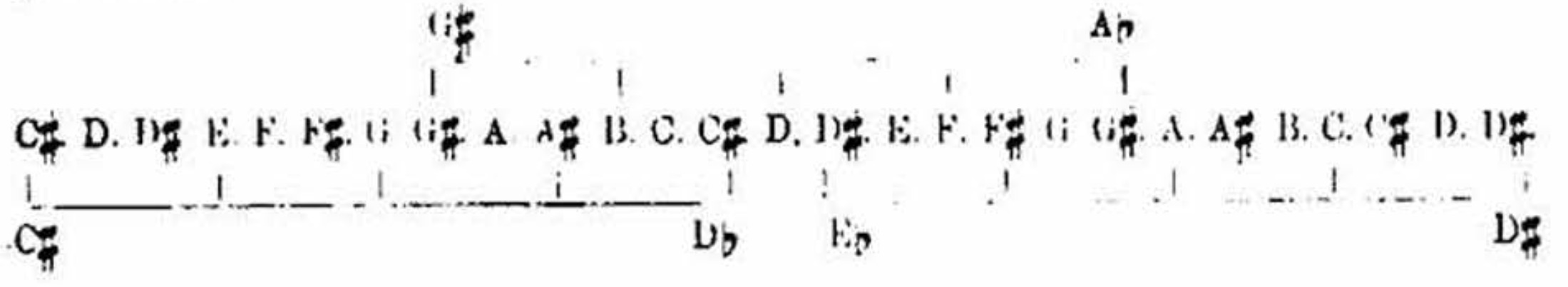
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
Under the symbol of a music plant this plate gives us to realize the growth-like continuity of chords and scales. The roots of the three chords of a key are represented in F, C, and G of the key of C. The plant might be represented as a creeping stem, like the creepers of the strawberry, with its progressive roots struck into the earth; but it is better to show an upward stem with aerial roots, for such are the roots of the musical plant. The main stem of the plant has the three chords, F a C e G b D; that is, F a c, C e g, G b d, the subdominant, tonic, and dominant. The terminal chord, D f# a, is to show that the keys as well as the chords GROW out of each other. Include the side branches which terminate with the octave notes of the chords, read thus - F a c f, G e g e, G b d g, because a chord is felt to be most complete in its unity when thus shut in by the octave note of its root. This is the reason why the great three-times-three chord does not stop at D, the top of the dominant chord, but goes on to the sixth octave of the fundamental root, shutting all in by the great peacemaker, F, in order to preserve the unity of the effect which this chord of chords produces. Before D. C. Ramsay showed that the scale of Harmonics extended to six octaves, it was by teachers of the science of music only extended to four. [Scientific Basis and Build of Music, page 110]
In the major system, when the tonic chord follows the subdominant one, there is one semitonic progression to the middle of the tonic, and one note in common with the root, so these two chords are linked together in different ways. When the tonic chord follows the dominant one, there is one semitonic progression to the root of the tonic, and one note in common with its top, so these two chords also are linked together in two different ways. When the tonic chord follows the compound dominant, i.e., the dominant seventh, there are two semitonic progressions, one to the middle and one to the root, and one note in common with its top, so these two are linked together in the same two ways; but the semitonic progression being double gives this resolution great urgency. And now we come to the two chords, the subdominant and dominant, which have no note in common, and must, when they succeed each other, be helped to come together. Nature teaches us how this is to be done by a process of borrowing and lending which will establish between them a similar relationship to that which keeps the continuity of the other chords in succession. We have seen that the top of the subdominant and the root of the tonic are a note in common to these chords, and so the top of the tonic and the root of the dominant also are a note possessed in common by these two chords. In like manner in this disjunct part, when the dominant follows the subdominant, the root of the subdominant is lent to the top of the dominant, and thus they come to have a note in common. The top of the [Scientific Basis and Build of Music, page 111]
subdominant also moves by semitonic progression to the middle of the dominant, and so, like the simple chords, they are brought into continuity. When the subdominant follows the dominant, the top of the dominant is lent to the root of the subdominant, and they come to have also a note in common; and the middle of the dominant moves by semitonic progression to the top of the subdominant; and thus resolving continuity is established between them. [Scientific Basis and Build of Music, page 112]
With perfect duality of response does resolution of chords go on in the minors. When the tonic chord follows the subdominant one, they have for their note in common A, i.e., in the key of A; and the middle of the subdominant moves by semitonic progression to the top of the tonic. When the tonic chord follows the dominant one, the top of the tonic and the root of dominant E is a note in common, and the top of the dominant goes by semitonic progression to the middle of the tonic. These simple chords are thus linked together exactly with the same degree of continuity as the simple chords of the major. When the tonic chord follows the compound subdominant, this compound chord, like the compound dominant in the major, has two semitonic progressions - one to the top and one to the middle of the tonic - and they have one note in common. When the compound dominant follows the subdominant, the root of the subdominant is lent to the top of the dominant, and thus a note in common is created, and the middle of the subdominant moves by semitonic progression to the root of the dominant. When the compound subdominant follows the dominant, the top is lent to the root of the subdominant, creating a note in common between them, and the root of the dominant goes to the middle of the subdominant in semitonic progression. This is the way of Nature. The unbroken continuity of her ways is perfectly illustrated in the linked sweetness and kinship of chords in a key; or when one key passes by modulation to another key; and that through all the chords and all the keys. We shall see wondrously more of this when we come to the study and contemplation of the Chromatic System of Chords. [Scientific Basis and Build of Music, page 112]
Hughes
the present, and the future, developing in geometric progression; as the past retires, the future advances. The rests in harmony correspond with silence in the Scriptures, both limiting and illimitable. But there is this essential difference: musical instruments can only be tuned to a certain pitch, whereas the Bible will never need fresh editions or corrections, but as it always has unfolded, it always will unfold, as it is necessary to meet our higher mental powers. I believe that, eventually, scientific minds will arrive at the conclusion that all the energies around us arise from the laws which regulate the life of matter, and cause the continual development of trinities from unities. Continuity everywhere adapts simple laws to wondrous workings. If we evade the belief in the development of trinities, this scheme falls to the ground. We can conceive no grander idea of the power, wisdom, and love of the Parent of the universe than that of His following out His own characteristics, knowing that at any moment, if His life-giving power were withdrawn, all would crumble into dust. Let us link with this thought these glorious promises— [Harmonies of Tones and Colours, Scripture Compared with Scripture, page 47]
Christ Returns - Speaks His Truth
"Male and female have also been individualised to experience and express WILLPOWER.
WILLPOWER in the MALE is experienced and expressed primarily as Activity. In primitive forms - he moves out into the environment to fulfill his INTENTION. Therefore, he dons the robes of the leader and quester. He was individualised to think and work to fulfill his purposes without the encumbrance of emotions.
WILLPOWER in the FEMALE is motivated and experienced primarily as Feeling - the Need to Nurture the original INTENTION and bring it, PURPOSE fully to full term - fruition - through the process of caring, feeding, clothing, repairing, teaching, protecting.
PURPOSE is entirely different to INTENTION since purpose comes down from the mental plane of intention and becomes an emotional drive, a desire to formulate 'a means to achieve the intended end'.
A 'powerful INTENTION to do something' becomes a PURPOSE behind continued existence. In this way, thought and feeling are married to perform the work of creation.
The male is constantly roaming seeking new ideas, new ways to fulfill his intentions to give him purpose in life.
The female's intentions are 'purpose personified', sensitive and stable, prepared to make sacrifices for the loved ones.
Therefore, the two basic IMPULSES within the SOURCE of BEING - expressed in physical form as male and female - are inter-dependent. One could not survive without the other. Both are needed for the continuity of creation.
Because of his masculine mobility, his leadership drive, the male has considered himself superior to the female. This is because she remains stable, creating security for the male. But the feminine drive is the drive of unconditional love, the drive worthy of the highest respect and consideration to enable her to flourish and perform her innate purpose within the household in peace of mind and joy.
The man's role is to provide physical security and material means of subsistence for the family.
The woman's role is to provide emotional security and the emotional means of personal fulfilment and joy within the family environment." [Christ Returns - Speaks His Truth, Letter 4, page 18]
Pond
"Love is perfect continuity without extension." [Dale Pond]
See Also
common chord
Continuous Motion
degree of continuity
Law of Continuity
permanence
triplet
9.11 - Love or Sympathy is Perfect Continuity
